Семплинг (сэмплинг)

Downsampling

Итак, при уменьшении частоты дискретизации упрощённо происходит два этапа:

1. Цифровая фильтрация сигнала для того, чтобы удалить высокочастотные составляющие, которые не удовлетворяют пределу Найквиста для новой частоты дискретизации;
2. Удаление или (отбрасывание) лишних отсчетов (сохраняется каждый N-й отсчёт). Здесь следует пояснить, что при программной реализации алгоритма децимации «лишние» отсчёты не удаляются, а просто не вычисляются (отбрасываются). При этом число обращений к цифровому фильтру уменьшается в определённое количество раз.

Так вот. Второй этап удаление или (отбрасывание) лишних отсчетов в англоязычной литературе иногда обозначают термином downsampling, что по сути может употребляться как синоним термина «децимация».

использовать

К музыкантам или продюсерам, которые начали сэмплирование первыми, относятся:

• Пьер Шеффер (1948, musique concrète )
• Базз Клиффорд (1960, Baby Sittin ‘Boogie )
• Джон Кейдж (1962, Уильям Микс )
• Уилл Брандес и Маленькая Элизабет — (1962, Baby Twist — голоса малышей Элизабет являются «образцами»)
• Битлз (1968, Revolution 9 )
• CAN (1969, в разрезе )
• Pink Floyd (1973, Деньги )
• Пульсирующий хрящ (1977, второй годовой отчет )
• Куртис Блоу (19?, Хип-хоп )
• Карлос Перон (1980 Solid Pleasure)
• Кейт Буш (1980, Бабушка )
• Хуберт Богнермайр , Харальд Зусацрадер (1981, «Эрденкланг»)
• Жан Мишель Жарр (1981, Магнитные поля )
• Брайан Ино (1981, Моя жизнь в кустах призраков )
• Питер Гэбриэл (1982, Shock The Monkey )
• Тревор Хорн и др. с искусством шума (1983)
• Да (1983, владелец одинокого сердца)
• Арно Штеффен (1983, хит )
• Катушка (1984, прозрачная )
• Причуда Гаджет (1984, Новые люди )
• Depeche Mode (1983, конвейер )
• Хольгер Хиллер (1983, Связка гнили в яме )
• Kraftwerk (1986, электрическое кафе )
• DJ Shadows Album Endtroduction ….. — первый альбом, состоящий только из сэмплов.
• Компьютерные жокеи стали первым коммерчески успешным чартерным коллективом в 1997 году с семплами и автономным компьютером (без дополнительного звукового генератора / MIDI) вживую со своими собственными аранжировками.
• Джон Освальд использовал в своей Plunderphonics впервые микро выборки , Акуфно это привело в доме на контексте

Frequently asked questions about sampling

What is sampling?

A sample is a subset of individuals from a larger population. Sampling means selecting the group that you will actually collect data from in your research. For example, if you are researching the opinions of students in your university, you could survey a sample of 100 students.

In statistics, sampling allows you to test a hypothesis about the characteristics of a population.

Why are samples used in research?

Samples are used to make inferences about populations. Samples are easier to collect data from because they are practical, cost-effective, convenient and manageable.

What is probability sampling?

means that every member of the target population has a known chance of being included in the sample.

Probability sampling methods include simple random sampling, systematic sampling, stratified sampling, and cluster sampling.

What is non-probability sampling?

In , the sample is selected based on non-random criteria, and not every member of the population has a chance of being included.

Common non-probability sampling methods include convenience sampling, voluntary response sampling, purposive sampling, snowball sampling, and quota sampling.

What is multistage sampling?

In multistage sampling, or multistage cluster sampling, you draw a sample from a population using smaller and smaller groups at each stage.

This method is often used to collect data from a large, geographically spread group of people in national surveys, for example. You take advantage of hierarchical groupings (e.g., from state to city to neighborhood) to create a sample that’s less expensive and time-consuming to collect data from.

What is sampling bias?

Sampling bias occurs when some members of a population are systematically more likely to be selected in a sample than others.

Примечания[править]

1. I. Mani, J. Zhang. “kNN approach to unbalanced data distributions: A case study involving information extraction,” In Proceedings of the Workshop on Learning from Imbalanced Data Sets, pp. 1-7, 2003.
2. D. Wilson, “Asymptotic Properties of Nearest Neighbor Rules Using Edited Data,” IEEE Transactions on Systems, Man, and Cybernetrics, vol. 2(3), pp. 408-421, 1972.
3. N. V. Chawla, K. W. Bowyer, L. O. Hall, W. P. Kegelmeyer, “SMOTE: Synthetic minority over-sampling technique,” Journal of Artificial Intelligence Research, vol. 16, pp. 321-357, 2002.
4. H. Han, W.-Y. Wang, B.-H. Mao, “Borderline-SMOTE: A new over-sampling method in imbalanced data sets learning,” In Proceedings of the 1st International Conference on Intelligent Computing, pp. 878-887, 2005.
5. H. M. Nguyen, E. W. Cooper, K. Kamei, “Borderline over-sampling for imbalanced data classification,” In Proceedings of the 5th International Workshop on computational Intelligence and Applications, pp. 24-29, 2009.
6. G. E. A. P. A. Batista, A. L. C. Bazzan, M. C. Monard, “Balancing training data for automated annotation of keywords: A case study,” In Proceedings of the 2nd Brazilian Workshop on Bioinformatics, pp. 10-18, 2003.
7. G. E. A. P. A. Batista, R. C. Prati, M. C. Monard, “A study of the behavior of several methods for balancing machine learning training data,” ACM Sigkdd Explorations Newsletter, vol. 6(1), pp. 20-29, 2004.
8. X.-Y. Liu, J. Wu and Z.-H. Zhou, “Exploratory undersampling for class-imbalance learning,” IEEE Transactions on Systems, Man, and Cybernetics, vol. 39(2), pp. 539-550, 2009.
9. C. Chao, A. Liaw, and L. Breiman. «Using random forest to learn imbalanced data.» University of California, Berkeley 110 (2004): 1-12.
10. Hido, Shohei & Kashima, Hisashi. (2008). Roughly Balanced Bagging for Imbalanced Data. 143-152. 10.1137/1.9781611972788.13.

Виды сэмплинга

Сэмплинг — отличный способ стимулирования продаж в ритейле. Его организация в точках продаж позволяет подключать эмоции потенциальных покупателей и мотивирует их делать спонтанные покупки. Однако, сэмплинг не обязательно проводят на территории магазина или торгового центра. Некоторые компании предлагают образцы своей продукции прямо на улице. Ознакомьтесь подробнее с видами сэмплинга.

• Обмен (Switch-sampling). Подразумевает обмен наполовину пустой упаковки используемого товара на новый. Такой подход помогает клиенту сравнить качество аналогичных товаров.
• Сухой сэмплинг (dry sampling). Предполагает рекламу продукта в точке продажи. Потенциальным покупателям предлагают взять с собой пробник бальзама для волос, крема, зубной пасты или другого товара.
• Влажный сэмплинг (wet sampling). Предоставляет целевой аудитории возможность продегустировать товар на месте. Например, колбасные изделия, сыр, масло, йогурт и так далее.
• HoReCa сэмплинг (Hotel-Restaurant-Cafe sampling). Это дегустация алкогольных и безалкогольных напитков, а также сигарет. Такой сэмплинг чаще всего организовывают в ресторанах, кафе, гостиницах и преподносят как комплимент от заведения или подарок при заказе на определенную сумму.
• Домашний сэмплинг (house-to-house sampling). Предполагает рассылку примеров товара почтой. Это может быть мини-версия продукта или печатная реклама с образцами и многое другое.

Теперь, когда вы знаете виды сэмплинга, самое время узнать, как правильно его организовать.

Как организовать сэмплинг

1. Установите цели и задачи сэмплинга
2. Подберите продукт и установите объем сэмпла
3. Выберите время проведения сэмплинга
4. Выберите место проведения сэмплинга
5. Соберите команду промоутеров

Чтобы организовать эффективный сэмплинг, воспользуйтесь следующими полезными рекомендациями.

Установите цели и задачи сэмплинга. Прежде чем приступать к организационным вопросам, подумайте, зачем вам нужна эта акция, чего вы хотите достичь с ее помощью. Подготовьте маркетинговый план и по пунктам пропишите пути достижения каждой задачи.

Подберите продукт и установите объем сэмпла

В этом вопросе важно полагаться на интересы и предпочтения целевой аудитории. Тщательно продумайте, что вы будете предлагать, как и в каком количестве

Пропишите расходы, необходимые для организации сэмплинга.

Выберите время проведения сэмплинга. Установите, когда лучше всего взаимодействовать с целевой аудиторией. Сэмплинг может проводится на протяжении всего дня или в какие-то определенные часы. Такой подход позволит сконцентрировать усилия на потенциальных покупателях и не распылять свои ресурсы.

Выберите место проведения сэмплинга. На основании данных о своей целевой аудитории выявите наиболее релевантные точки проведения акции. Подумайте, где больше всего ваших потенциальных покупателей. При этом помните, что клиент должен иметь возможность купить товар, иначе он может передумать и все усилия будут сведены к минимуму.

Соберите команду промоутеров. В этом вопросе важно учесть пол, возраст и другие характеристики, которые могут влиять на уровень доверия вашей целевой аудитории.

При правильном подходе сэмплинг способен увеличить объем продаж на 200-300%. Однако, эффективность не всегда можно измерить в денежном эквиваленте, ведь ознакомление целевой аудитории с продукцией это еще и работа на перспективу. Используйте инструменты ATL и BTL-рекламы, задействуйте мессенджеры и социальные сети, чтобы увеличить количество точек контакта с клиентом.

Probability sampling methods

Probability sampling means that every member of the population has a chance of being selected. It is mainly used in quantitative research. If you want to produce results that are representative of the whole population, probability sampling techniques are the most valid choice.

There are four main types of probability sample.
 

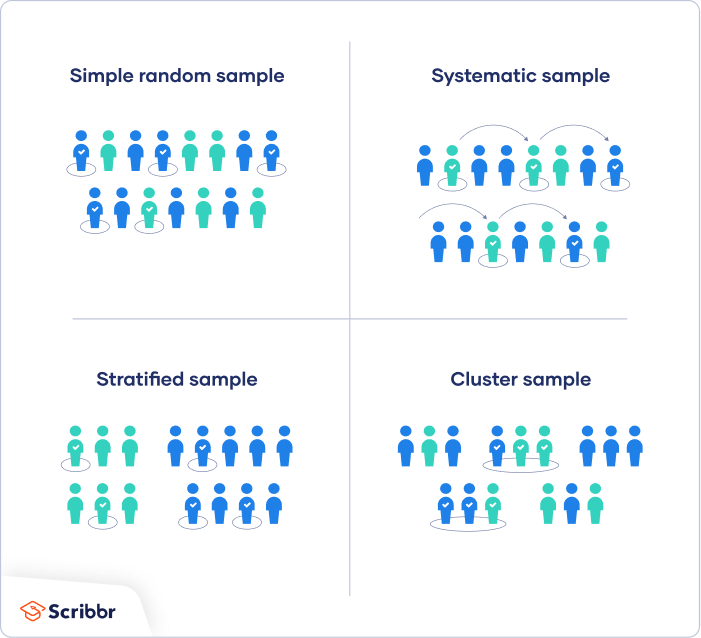
1. Simple random sampling

In a simple random sample, every member of the population has an equal chance of being selected. Your sampling frame should include the whole population.

To conduct this type of sampling, you can use tools like random number generators or other techniques that are based entirely on chance.

Example

You want to select a simple random sample of 100 employees of Company X. You assign a number to every employee in the company database from 1 to 1000, and use a random number generator to select 100 numbers.

2. Systematic sampling

Systematic sampling is similar to simple random sampling, but it is usually slightly easier to conduct. Every member of the population is listed with a number, but instead of randomly generating numbers, individuals are chosen at regular intervals.

Example

All employees of the company are listed in alphabetical order. From the first 10 numbers, you randomly select a starting point: number 6. From number 6 onwards, every 10th person on the list is selected (6, 16, 26, 36, and so on), and you end up with a sample of 100 people.

If you use this technique, it is important to make sure that there is no hidden pattern in the list that might skew the sample. For example, if the HR database groups employees by team, and team members are listed in order of seniority, there is a risk that your interval might skip over people in junior roles, resulting in a sample that is skewed towards senior employees.

3. Stratified sampling

Stratified sampling involves dividing the population into subpopulations that may differ in important ways. It allows you draw more precise conclusions by ensuring that every subgroup is properly represented in the sample.

To use this sampling method, you divide the population into subgroups (called strata) based on the relevant characteristic (e.g. gender, age range, income bracket, job role).

Based on the overall proportions of the population, you calculate how many people should be sampled from each subgroup. Then you use random or systematic sampling to select a sample from each subgroup.

Example

The company has 800 female employees and 200 male employees. You want to ensure that the sample reflects the gender balance of the company, so you sort the population into two strata based on gender. Then you use random sampling on each group, selecting 80 women and 20 men, which gives you a representative sample of 100 people.

4. Cluster sampling

Cluster sampling also involves dividing the population into subgroups, but each subgroup should have similar characteristics to the whole sample. Instead of sampling individuals from each subgroup, you randomly select entire subgroups.

If it is practically possible, you might include every individual from each sampled cluster. If the clusters themselves are large, you can also sample individuals from within each cluster using one of the techniques above. This is called multistage sampling.

This method is good for dealing with large and dispersed populations, but there is more risk of error in the sample, as there could be substantial differences between clusters. It’s difficult to guarantee that the sampled clusters are really representative of the whole population.

Example

The company has offices in 10 cities across the country (all with roughly the same number of employees in similar roles). You don’t have the capacity to travel to every office to collect your data, so you use random sampling to select 3 offices – these are your clusters.

Receive feedback on language, structure and layout

Professional editors proofread and edit your paper by focusing on:

• Academic style
• Vague sentences
• Grammar
• Style consistency

Пример (задача о моллюсках)

Сравним практически некоторые из описанных стратегий на наборе данных про моллюсков (набор данных взят с UCI machine learning repository). В нем представлены физиологические сведения об этих животных. Имеются следующие поля:

1. пол;
2. длина;
3. диаметр (линия, перпендикулярная длине);
4. высота;
5. масса всего моллюска;
6. масса без раковины;
7. масса всех внутренних органов (после обескровливания);
8. масса раковины (после высушивания);
9. зависимая переменная: количество колец (в год на раковине моллюска появляется 1,5 кольца).

Изначально набор данных предназначен для решения задачи регрессии. По количеству колец на раковине определяется возраст моллюска. Для классификации в условиях несбалансированности создадим новую выходную переменную, принимающую только два значения. Для этого, предположим, что если количество колец у моллюска не превосходит 18, то для нас он будет считаться молодым, в противном случае – старым.

Также проимитируем ситуацию различия издержек и рассмотрим случаи, когда неверное отнесение старого моллюска к молодым может принести бо́льшие издержки, чем в случае неверной классификации фактически молодого.

Таким образом, мы получили набор данных с сильно несбалансированными классами, где значение «молодой» было присвоено 4083 записям (97,7%), а значение «старый» – 94 записям (2,3%). Далее стратифицированным сэмплингом были получены тестовый и обучающий наборы данных.

Прежде чем восстанавливать баланс между классами, вернемся к понятию издержек классификации. Во многих приложениях, таких как кредитный скоринг, директ-маркетинг, издержки при ложноположительной ($С_{10}$) классификации в несколько раз выше, чем при ложноотрицательной (обозначим их как $С_{01}$). При пороге отсечения 0,5 количество миноритарных примеров необходимо увеличить в $С_{10}/С_{01}$ раз (при условии что $С_{00} = С_{11} = 0$). Либо во столько же уменьшить мажоритарный класс (теоретическое обоснование этого утверждения изложено в работе ).

Сравним следующие подходы к восстановлению баланса между классами: случайное удаление примеров мажоритарного класса, дублирование примеров миноритарного класса, специальные методы увеличения числа примеров (алгоритмы SMOTE и ASMO).

Для алгоритмов SMOTE и ASMO количество ближайших соседей для генерации примеров установим равным 5.

Алгоритм ASMO признал набор данных нерассеянным (среди 100 ближайших соседей не нашлось даже 20 примеров из мажоритарного класса). Однако проигнорируем это сообщение и посмотрим, какой будет результат, если генерировать примеры, используя записи из каждого класса. Для кластеризации применен алгоритм k-means (k = 5).

После восстановления баланса строилась логистическая регрессия с порогом отсечения 0,5, и подсчитывались издержки. Результаты представлены на рисунке 7.

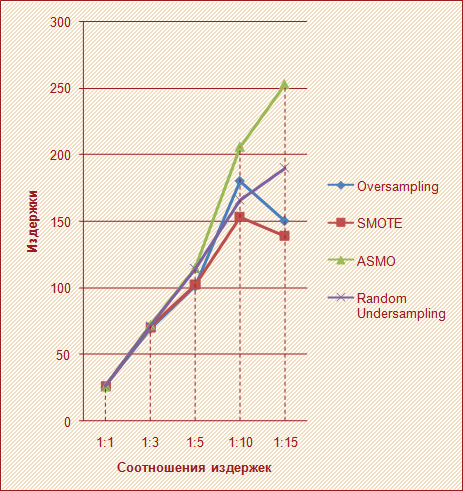
Из рисунка 6 видно, что наилучшим образом показал себя алгоритм SMOTE, так как издержки в данном случае оказались самыми меньшими. ASMO проявил себя хуже, однако стоит напомнить, что набор данных не рассеян и согласно данной стратегии необходимо было использовать SMOTE.

Итак, мы рассмотрели различные подходы сэмплинга для решения проблемы несбалансированности классов. Помимо него существуют стратегии, согласно которым происходит модификация алгоритма обучения, но их рассмотрение выходит за рамки данной статьи.

В таблице 1 приведено описание файлов с наборами данных, которые использовались в примере. Их можно найти в архиве.

Таблица 1 – Наборы данных

Описание набора данных	Файл
Исходный набор данных: Abalone Data Set (классы не выделены)	abalone_data.txt
Исходный обучающий набор данных	dataset75.txt
Тестовый набор данных	testdataset.txt
Набор данных с искусственными примерами. Алгоритм SMOTE. Соотношение издержек 1:3	syntsmote1_3.txt
Набор данных с искусственными примерами. Алгоритм SMOTE. Соотношение издержек 1:5	syntsmote1_5.txt
Набор данных с искусственными примерами. Алгоритм SMOTE. Соотношение издержек 1:10	syntsmote1_10.txt
Набор данных с искусственными примерами. Алгоритм SMOTE. Соотношение издержек 1:15	syntsmote1_15.txt
Набор данных с искусственными примерами. Алгоритм ASMO. Соотношение издержек 1:3	syntasmot1_3.txt
Набор данных с искусственными примерами. Алгоритм ASMO. Соотношение издержек 1:5	syntasmot1_5.txt
Набор данных с искусственными примерами. Алгоритм ASMO. Соотношение издержек 1:10	syntasmot1_10.txt
Набор данных с искусственными примерами. Алгоритм ASMO. Соотношение издержек 1:15	syntasmot1_15.txt

Different Types of Sampling Techniques

Here comes another diagrammatic illustration! This one talks about the different types of sampling techniques available to us: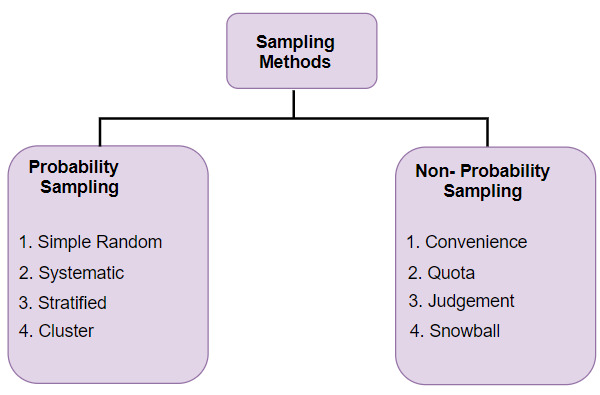

• Probability Sampling: In probability sampling, every element of the population has an equal chance of being selected. Probability sampling gives us the best chance to create a sample that is truly representative of the population
• Non-Probability Sampling: In non-probability sampling, all elements do not have an equal chance of being selected. Consequently, there is a significant risk of ending up with a non-representative sample which does not produce generalizable results

For example, let’s say our population consists of 20 individuals. Each individual is numbered from 1 to 20 and is represented by a specific color (red, blue, green, or yellow). Each person would have odds of 1 out of 20 of being chosen in probability sampling.

With non-probability sampling, these odds are not equal. A person might have a better chance of being chosen than others. So now that we have an idea of these two sampling types, let’s dive into each and understand the different types of sampling under each section.

Introduction

Here’s a scenario I’m sure you are familiar with. You download a relatively big dataset and are excited to get started with analyzing it and building your machine learning model. And snap – your machine gives an “out of memory” error while trying to load the dataset.

It’s happened to the best of us. It’s one of the biggest hurdles we face in data science – dealing with massive amounts of data on computationally limited machines (not all of us have Google’s resource power!).

So how can we overcome this perennial problem? Is there a way to pick a subset of the data and analyze that – and that can be a good representation of the entire dataset?

Yes! And that method is called sampling. I’m sure you’ve come across this term a lot during your school/university days, and perhaps even in your professional career. Sampling is a great way to pick up a subset of the data and analyze that. But then –  should we just pick up any subset randomly?

Well, we’ll discuss that in this article. We will talk about eight different types of sampling techniques and where you can use each one. This is a beginner-friendly article but some knowledge about descriptive statistics will serve you well.

If you’re new to statistics and data science, I encourage you to check out our two popular courses:

• Introduction to Data Science
• Applied Machine Learning: Beginner to Professional

Стратегии сэмплирования[править]

• Cубдискретизация (англ. under-sampling) — удаление некоторого количества примеров мажоритарного класса.
• Передискретизации (англ. over-sampling) — увеличение количества примеров миноритарного класса.
• Комбинирование (англ. сombining over- and under-sampling) — последовательное применение субдискретизации и передискретизации.
• Ансамбль сбалансированных наборов (англ. ensemble balanced sets) — использование встроенных методов сэмплирования в процессе построения ансамблей классификаторов.

Также все методы можно разделить на две группы: случайные (недетерминированные) и специальные (детерминированные).

• Случайное сэмплирование (англ. random sampling) — для этого типа сэмплирования существует равная вероятность выбора любого конкретного элемента. Например, выбор 10 чисел в промежутке от 1 до 100. Здесь каждое число имеет равную вероятность быть выбранным.
  • Сэплирование с заменой (англ. sampling with replacement) — здесь элемент, который выбирается первым, не должен влиять на вторую или любую другую выборку. Математически, ковариация равна нулю между двумя выборками. Мы должны использовать выборку с заменой, когда у нас большой набор данных. Потому что, если мы используем выборку без замены, то вероятность для каждого предмета, который будет выбран, будет изменяться, и она будет слишком сложной после определенного момента. Выборка с заменой может сказать нам, что чаще встречается в наших данных.
  • Сэмплирование без замены (англ. sampling without replacement) — здесь то, что мы выбираем первым, повлияет на второе. Выборка без замены полезна, если набор данных мал. Математически, ковариация между двумя выборками не равна нулю.
• Стратифицированное сэмплирование (англ. stratified sampling) — в этом типе техники мы выбираем из определенной группы объектов из всей выборки. Из каждой группы извлекается одинаковое количество объектов, хотя группы имеют разные размеры. Кроме того, существует вариант, когда количество объектов, выбранных из каждой группы, пропорционально размеру этой группы.

Сэмплирование Бернулли-Томпсона

Давайте в качестве введения, и чтобы легче было работать, упростим задачу с поиском розетки. Вместо того, чтобы каждая розетка возвращала разное количество заряда, пусть они либо заряжают, либо нет. Тогда у вознаграждения будет два возможных значения: 1 — розетка заряжает, 0 — розетка не заряжает. Если у случайной величины лишь два возможных значения, её поведение можно описать с помощью распределения Бернулли.

Теперь вместо количества энергии в розетках меняется вероятность заряжания как такового. Нам нужно найти розетку с максимальной вероятностью заряжания, а не розетку с максимальным количеством энергии.

Итак, при сэмплировании Томпсона получается модель вероятностей вознаграждения. Когда доступность вознаграждения является бинарной (как в этом случае, да или нет), идеальной моделью для такой вероятности является бета-распределение. Подробнее о взаимосвязи бета-распределения и распределения Бернулли читайте здесь.

Бета-распределение зависит от двух параметров: и . Проще говоря, это счётчики числа успехов и неудач. Также у бета-распределения есть усреднённое значение, вычисляемое как: 

Изначально мы не знаем, какова вероятность наличия энергии в какой-либо розетке, потому можно присвоить альфе и бете значение 1, что даст нам равномерное распределение (на иллюстрации 1 показано красным). Это начальное предположение называется априорной вероятностью: вероятность возникновения какого-то события до того, как мы получили какие-либо сведения о нем; в данном случае она представлена бета-распределением

Проверив розетку и получив вознаграждение, мы можем скорректировать наши ожидания того, что розетка работает. Такая новая вероятность после получения каких-то сведений называется апостериорной вероятностью. Она тоже представлена бета-распределением, но теперь мы обновили значения и на основе полученного вознаграждения.

Если розетка работает, то вознаграждение равно 1, и — счётчик успехов — увеличивается на 1. — счётчик неудач — не растёт. Если же мы не получим вознаграждение, то не изменится, а увеличится на 1. Чем больше мы собираем данных, тем сильнее бета-распределение начинает отличаться от прямой линии и становится всё более точной моделью вероятности усреднённого вознаграждения. Поддерживая значения и , алгоритм сэмплирования Томпсона может описать ожидаемое среднее вознаграждение и уровень его достоверности.

В отличие от жадного алгоритма, в котором на каждом временном шаге выбирается действие с наивысшим ожидаемым вознаграждением, даже если достоверность ожидания невысока, сэмплирование Томпсона берёт образцы из бета-распределения каждого действия, и выбирает действие с наивысшим возвращённым значением. Поскольку редко пробуемые действия имеют широкие распределения, (см. синюю кривую на иллюстрации 1), то у них больше диапазон возможных значений. Поэтому розетка, у которой сейчас низкое ожидаемое среднее вознаграждение, но которая тестировалась реже розетки с более высоким средним ожиданием, может вернуть большее выборочное значение и будет выбрана на следующем временном шаге.

На вышеприведённом графике синяя кривая имеет более низкое ожидаемое среднее вознаграждение, чем у зелёной кривой. Поэтому при жадном алгоритме будет выбрана зелёная розетка, а синяя никогда не будет выбрана. А сэмплирование Томпсона эффективно учитывает полную ширину кривой, которая у синей розетки может быть шире, чем у зелёной. В этом случае выбор может быть сделан в пользу синей розетки.

Чем чаще используется розетка, тем выше достоверность её ожидаемого среднего. Это отражено в сужении распределения вероятности, и выборочное значение будет браться из диапазона значений, которые ближе к реальному среднему (см. зелёную кривую на иллюстрации 1). В результате исследование (explore) уменьшается, а использование (exploit) растёт, потому что алгоритм начинает чаще выбирать розетки с более высокой вероятностью получения вознаграждения.

С другой стороны, розетки с низким ожидаемым среднем будут выбираться реже и в конце концов будут быстро выброшены из процесса выбора. Поэтому их истинное среднее может и не быть найдено. А поскольку нас интересует лишь розетка с наивысшей вероятностью получения вознаграждения, причём найти её нужно как можно скорее, то нас не волнует, что мы так и не получим всю информацию о плохо работающих розетках. 

Результаты экспериментов

Как и в случае с Бернулли, мы прогнали больше 1000 попыток. Поскольку апостериорное распределение началось с почти прямой линии, каждая из пяти розеток однократно проверена в течение первых пяти попыток. В последующих попытках доминирует розетка 4 (красная кривая). К концу тестирования она превратилась в высокую тонкую кривую, центр которой лежит на значении 12 (истинное значение вознаграждения розетки), что говорит о высоком уровне достоверности этого значения.

За первые 200 проверок лишь ещё одна розетка тестировалась больше одного раза — пятая (фиолетовая кривая, с истинным вознаграждением 10). Но она проверялась лишь трижды, поэтому имеет маленькую и толстую кривую распределения, что говорит о низкой достоверности значения.

Иллюстрация 3: сэмплирование Томпсона с использованием нормального распределения для пяти розеток, с истинными значениями вознаграждения 6, 4, 8, 12 и 10 соответственно.

На иллюстрации 3 видно, как быстро сэмплирование Томпсона находит и использует лучшую розетку, а остальные оставляет практически без проверки. Таким образом алгоритм возвращает большое и почти оптимальное накопленное вознаграждение.

Реализация розеток по Бернулли

Воспользуемся базовым классом розеток, поверх которого добавим особую функциональность изучаемого алгоритма. Затем прогоним этот новый класс через набор экспериментов с помощью тестовой программы для всех бандитских алгоритмов. Подробное описание базового класса розеток и тестовой системы дано в одной из предыдущих статей, а весь код лежит на Github.

Покажу реализацию сэмплирования Бернулли-Томпсона на примере класса :

В этом классе мы инициализируем и со значениями 1, чтобы получить равномерное распределение. Затем при обновлении мы просто увеличиваем если розетка возвращает вознаграждение, а в противном случае увеличиваем .

Функция sample выводит значение из бета-распределения, используя в качестве параметров текущие значения и .

Классификация методов сэмплинга

Общепринятая классификация методов сэмплинга представлена на рис. 2.

Рисунок 2. Классификация методов сэмплинга

Все методы сэмплинга делятся на две группы — детерминированные и вероятностные (probability sampling) или случайные (random sampling). В детерминированных методах процесс формирования выборки производится в соответствии с формально заданными правилами и ограничениями. Например «выбрать всех мужчин в возрасте от 30 до 40 лет». Тогда все объекты, удовлетворяющие правилу будут помещены в выборку обязательно. В вероятностных методах для каждого объекта определяется вероятность, с которой он может быть взят в выборку.

Oversampling

И децимацию и интерполяцию уже упомянули. Вроде бы и всё. Но в плагинах часто можно увидеть термин oversampling, да ещё и с каким-то настройками. Давайте разбираться.

Есть такое определение как «Дискретизация сигналов с запасом по частоте дискретизации». То есть применяется дискретизация сигнала на частоте, в несколько раз превышающей частоту Котельникова (предел Найквиста) с последующей децимацией. Вот она и называется в англоязычной литературе термином oversampling.

Например, возьмём сигнал с шириной полосы или самой высокой частотой B  = 100  Гц. Зная, что есть предел Найквиста берётся частота дискретизации в 2 раза больше — 200 Гц (100 × 2). При oversampling 4x частота дискретизации в четыре раза превышает частоту дискретизации 800 Гц (200 × 4). В итоге фильтр anti — aliasing работает в переходной полосе 300 Гц. То есть получается следующая формула (( f _s / 2) — B  = (800 Гц / 2) — 100 Гц = 300 Гц.

Что даёт такой тип дискретизации сигнала?

1. Возможность использовать АЦП (аналого-цифровой преобразователь) с меньшей разрядностью.
2. Возможность использовать более простой и дешёвый аналоговый фильтр для защиты от наложения спектров.
3. Подобная передискретизация способна улучшить разрешение и отношение сигнал / шум, а также может помочь избежать наложения спектров и фазовых искажений путем ослабления требований к характеристикам фильтра сглаживания.

Аналогичный подход применяется и при восстановлении сигнала по его отсчётам.

What is Sampling?

Let’s start by formally defining what sampling is.

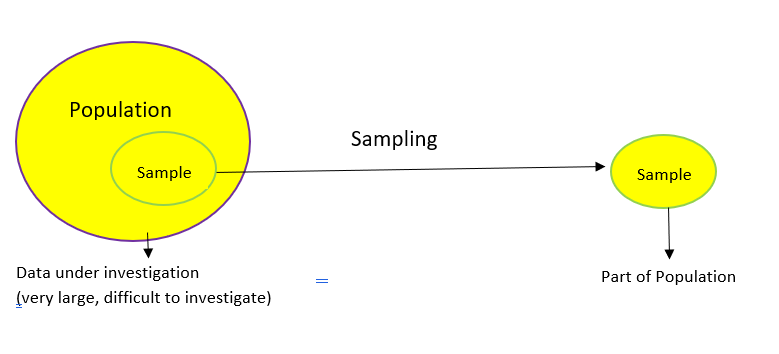
The above diagram perfectly illustrates what sampling is. Let’s understand this at a more intuitive level through an example.

We want to find the average height of all adult males in Delhi. The population of Delhi is around 3 crore and males would be roughly around 1.5 crores (these are general assumptions for this example so don’t take them at face value!). As you can imagine, it is nearly impossible to find the average height of all males in Delhi.

It’s also not possible to reach every male so we can’t really analyze the entire population. So what can we do instead? We can take multiple samples and calculate the average height of individuals in the selected samples.

But then we arrive at another question – how can we take a sample? Should we take a random sample? Or do we have to ask the experts?

Let’s say we go to a basketball court and take the average height of all the professional basketball players as our sample. This will not be considered a good sample because generally, a basketball player is taller than an average male and it will give us a bad estimate of the average male’s height.

Here’s a potential solution – find random people in random situations where our sample would not be skewed based on heights.

Основные этапы построения выборки

Какой-либо универсальной, подходящей для всех задач анализа, последовательности действий при реализации процесса сэмплинга, вообще говоря, указать нельзя. Но наиболее типичной является следующая последовательность шагов.

Определение генеральной совокупности. На данном этапе аналитик должен определить из каких объектов будет состоять совокупность (людей, домохозяйств, предприятий, товаров и т.д.), какими признаками они характеризуются, а также произвести географическую и временную привязку. В некоторых случаях может возникнуть ситуация, когда совокупность может содержать наблюдения, которые будут являться следствием наблюдением другой совокупности (суперсовокупности). При этом совокупность и суперсовокупность могут частично перекрываться.

Определение основы выборки (sampling frame). В простейшем случае, в выборку может быть включен любой элемент совокупности — это называется прямым отбором. Однако на практике может оказаться полезным сформировать так называемую основу выборки — часть генеральной совокупности, элементы которой удовлетворяют требованиям решаемой задачи. Например, это могут быть люди старше 18 лет, клиенты с доходом выше среднего по региону и т.д. Возможно требование, чтобы каждый элемент совокупности попадал в основу выборки только один раз. Применяется показатель инцидентности (охвата) выборки, равный процентной доле генеральной совокупности, которая будет использоваться для отбора.

Выбор метода и алгоритма сэмплинга (план выборки). Этот выбор не всегда очевиден и однозначен. На практике приходится использовать опыт решения аналогичных задач, либо выбирать лучший метод экспериментально. Кроме этого выбранный метод зависит от типа данных и количества объектов.

Определение объёма выборки. Зависит от многих факторов. Например, в статистических методах исследования объём выборки должен обеспечивать возможность оценки законов распределения данных и их параметров. В машинном обучении объём обучающей выборки должен обеспечивать её полноту и репрезентативность, а также может зависеть от особенностей модели. Например, число примеров обучающей выборки для обучения нейронной сети должно превышать число межнейронных связей, которые настраиваются в процессе обучения. В противном случает сеть не приобретёт обобщающей способности.

Реализация процесса сэмплинга. Также имеет свои особенности. Например отбор наблюдений может производится из локальных или удалённых источников. Во втором случае процесс извлечения выборок больших объёмов может сопровождаться повышением нагрузки на сеть компании. Поэтому его лучше реализовывать в соответствии с наиболее безопасным временным регламентом

Кроме этого в процессе сэмплинга может произойти разрыв соединения, поэтому важно, чтобы после его восстановления процесс можно было продолжить, а не начинать сначала.

Сбор данных по отобранным объектам (если это необходимо). В некоторых случаях в процессе сэмплинга отбираются только идентификаторы объектов

Например, клиенты для опроса могут сначала отбираться по номерам клиентских карт, а потом в ходе опроса определяются их пол, возраст, доход и т.д.