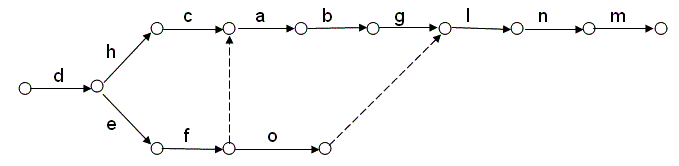Пример построения сетевого графика

Построение сетевого графика

В нашем примере для построения сетевого графика необходимо составить формуляр операций, его можно использовать в качестве образца на практике.

В таблицу сведем следующие данные по каждой операции:

• номер операции;
• предшествующие операции;
• количество исполнителей;
• продолжительность операции в днях.

В таблице операций их номера соответствует нумерации в карточке-определителе в соответствии с группировкой параллельных операций.

Таблица операций для построения сетевого графика

Номер операции	Предыдущие операции	Кол-во исполнителей, чел.	Продолжительность, дни
1.	—	10	1
2.	1	2	3
3.	1	3	1
4.	1	2	4
5.	4	1	0,5
6.	3	3	2
7.	5	2	0,5
8.	2,7,6	10	0,5
9.	9	10	0,5
10.	9	1	3
11.	9	2	4
12.	9	2	2
13.	9	2	3
14.	12	2	2
15.	13	3	2
16.	10,11,14,15	10	0,5
17.	16	10	0,5
18.	17	2	2
19.	18	2	3
20.	17	2	2
21.	17	2	3
22.	21	3	1
23.	20	2	2
24.	19,22,23	10	0,5
25.	24	10	0,5
26.	25	5	1
27.	26	5	3
28.	25	3	2
29.	28	3	2
30.	25	2	4
31.	27,29,30	10	0,5
32.	31	10	0,5
33.	32	7	1
34.	32	2	1
35.	33,34	10	1

На основе таблицы операций и карточки-определителя с учетом произведенной группировки параллельных операций осуществляется построение сетевого графика.

Сетевой график, пример

Определим критический путь. Критический путь на данном сетевом графике составляют операции: 1, 4, 5, 7, 8, 9, 13, 15, 16, 17, 18, 19, 24, 25, 28, 29, 31, 32, 33 (34), 35.

В результате построения сетевого графика работы можно сделать вывод, что деятельность организации не укладывается в заданный срок равный 22 рабочим дням, составляя вместо этого 26 дней. При этом операции первой, второй и третьей недели не укладываются в заданный для них срок, равный 5 рабочим дням. По сетевой модели операции 1 недели длятся 7 дней, 2 недели – 6 дней, 3 недели – 6 дней. Операции четвертой и пятой недель укладываются в заданные для них сроки.

Для соблюдения запланированных сроков произведем корректировку сетевого графика.

В нашем примере сетевого графика по данным карточки-распределителя можно сделать вывод, что для некоторых операций в рамках запланированных действий существует резерв специалистов в отделе. Учитывая, что общая численность сотрудников относительно невелика, можно воспользоваться способом корректировки сетевой модели с привлечением дополнительных ресурсов, в качестве которых выступают свободные на момент реализации операции специалисты данного отдела. Благодаря этому сократится срок выполнения операций критического пути, соответственно и сроки всей сетевой модели. Корректировке подлежат операции 1, 2 и 3 недель, так как операции 4 и 5 недель сетевого графика укладываются в заданные сроки.

После корректировки осуществим построение альтернативного сетевого графика.

Необходимо привлечь дополнительных специалистов для выполнения операций 4 (отдел специальных программ), 13 (отдел по организации оздоровительной кампании) и 18 (отдел специальных программ). Расчет трудоемкости операций (Q) определим исходя из произведения числа специалистов (N), выполняющих операцию, на число дней (t), выделенных для ее выполнения:

Q = N * t

Q4 = 2*4 = 8 ч/дн

Q13 = 2*3 = 6 ч/дн

Q18 = 2*2 = 4 ч/дн

В отделе специальных программ работает 5 человек, но в выполнении операции 4 задействовано только 2 человека. В результате привлечения двух специалистов новый срок выполнения операции составит: 8 / 4 = 2 дня. Следовательно, операция 4 будет выполняться 2 дня вместо 4 дней.

В отделе по организации оздоровительной кампании работает 3 специалиста, но в выполнении операции 13 занято только два человека. В данном случае привлечение одного дополнительного специалиста позволит сократить срок выполнения операции: 6 / 3 = 2 дня. Следовательно, операция 13 будет выполняться 2 дня вместо 3 дней.

В выполнении операции 18 задействовано 2 специалиста отдела специальных программ. Привлечение двух дополнительных специалистов позволит сократить срок ее выполнения: 4 / 4 = 1 день. Следовательно, операция 18 будет выполняться 1 день вместо 2 дней.

В результате получаем срок выполнения операций после корректировки сетевого графика с привлечением дополнительных ресурсов:

26 – 2 – 1 – 1 = 22 дня.

Таким образом, за счет произведенной коррекции сетевого графика срок выполнения операций, соответствует изначально заданному сроку в 22 рабочих дня.

Альтернативный график будет аналогичен предыдущему в плане своей структуры, корректировке подвергнуты сроки реализации операций согласно построенной сетевой модели.

Альтернативный сетевой график

Автоматическая сетевая диаграмма проекта с критическим путем в EXCEL

Построим автоматическую сетевую диаграмму проекта. Сетевую диаграмму изобразим на диаграмме MS EXCEL типа Точечная. На этой диаграмме выведем работы проекта в виде точек, стрелками изобразим связи между работами. Также изобразим на диаграмме критический(ие) путь(и). Сетевая диаграмма будет автоматически перестраиваться при изменении связей между работами и их длительности.

Данная статья является третьей статьей в цикле статей посвященных построению сетевой диаграммы проекта и является синтезом первых двух:

1. В статье Метод критического пути в MS EXCEL показано как рассчитать длительность проекта, определить работы на критическом пути и как построить сетевую диаграмму проекта на листе MS EXCEL. Основной недостаток – при изменении связей между работами пользователю потребуется вносить серьезное изменение в сетевую диаграмму.
2. В статье Автоматическая сетевая диаграмма проекта в MS EXCEL показано, как имея перечень работ и связи между ними, вычислить все пути проекта и отобразить их на стандартной диаграмме типа Точечная. При изменении связей – пути автоматически пересчитываются. Однако, критический путь не вычислялся в этой статье.

Рекомендуется прочитать вышеуказанные статьи перед первым прочтением.

Ниже показана диаграмма, которую мы будем создавать в этой статье. На диаграмме отображены все работы проекта (от А до U, синие точки), связи между ними (стрелки), работы на критическом пути (красные точки), критический путь (красные стрелки).

Примечание : Слово диаграмма используется в 2-х смыслах: сетевая диаграмма проекта (стандартный термин из управления проектом, Activity-on-node diagram ) и диаграмма MS EXCEL ( Excel Chart , см. вкладку , группа ). Диаграмма MS EXCEL типа Точечная будет использоваться для построения сетевой диаграммы проекта.

При изменении связей между работами и/или их длительности происходит перерасчет критического пути и сетевая диаграмма автоматически обновляется. Например, значительное увеличение длительности работы М (в нижнем пути сетевой диаграммы) приведет к изменению критического пути.

Такая сетевая диаграмма отображает критический путь даже нагляднее, чем стандартная диаграмма Ганта , хотя, конечно, не заменяет ее.

ВНИМАНИЕ! Построение данной сетевой диаграммы в этой статье приведено лишь с целью демонстрации технической реализуемости такого построения в MS EXCEL. Не ставилось целью сделать “удобную программу для пользователей”

Это означает, что при изменении пользователем количества работ/ добавления связей между работами (например, использования более 5 последователей), переименовании листов, рядов диаграммы и других изменений, в файле примера может потребоваться дополнительная настройка формул.

Такая настройка потребует от пользователя серьезных знаний MS EXCEL и времени.

Исходная информация

В качестве исходной информации дан перечень работ, их длительность и связи между работами.

Также вручную задаются координаты для отображения на диаграмме работ (диапазон ВА12:ВВ34 ).

Другой информации для построения сетевой диаграммы и вычисления критического пути не требуется.

Вычисление путей сетевой диаграммы

Как и в статье Автоматическая сетевая диаграмма проекта в MS EXCEL начнем построение сетевой диаграммы с вычисления путей.

В отличие от указанной статьи, здесь увеличено количество рассчитываемых путей (до 15) и максимальная длина путей (до 10 работ, включая вехи начала и окончания).

Алгоритм вычисления путей аналогичен, однако формулы изменены, чтобы позволить пользователю быстро увеличивать количество путей проекта и их длину.

Начиная с шага №1 (начиная со строки 96) формулы можно копировать вниз и вправо, чтобы при необходимости увеличить количество путей и их длину (количество шагов). На каждом шаге длина путей увеличиваются на одну работу. В случае наличия нескольких последователей у работы – увеличивается количество возможных путей.

После вычисления всех шагов, в диапазоне R62:AA76 выводится перечень всех путей проекта, содержащие входящие в них работы.

Построение сетевой диаграммы

Сначала на диаграмме выводятся работы (синие точки, ряд Работы ).

Затем выводятся все возможные пути проекта (ряды Путь_1, Путь_2, …, Путь_15 ).

Все работы, находящиеся на критическом пути, отмечаются красным цветом. Также на диаграмму выводится критический путь. Если путей несколько, то выводятся все пути (в файле примера выводятся максимум 3 критических пути). Если длительность работы О увеличить до 8 дней, то 3 пути станут критическими с длительностью по 65 дней.

Одновременно, работы проекта отображаются на диаграмме Ганта.

Расчет графика: прямой анализ

Оценка временных затрат на выполнение одной операции производится на основании нормативных трудозатрат. Благодаря прямому или обратному методу расчета, можно довольно быстро сориентироваться в порядке выполнения работ и выявить критические шаги.

Прямой анализ позволяет определить ранние сроки начала всех операций. Обратный — дает представление о поздних сроках. Кроме того, с помощью обеих методик анализа можно не только установить критический путь, но и выявить временные интервалы, на которые можно задержать выполнение отдельных работ без срыва общих сроков реализации проекта.

Прямой анализ рассматривает проект от начала до конца (если говорить о составленном графике, то движение по нему происходит слева направо). Во время движения по всем цепочкам операций происходит наращение времени выполнения всего комплекса работ. Прямой расчет сетевого графика предполагает, что каждая последующая операция начинается в тот момент, когда заканчиваются все предшествующие ей. При этом необходимо помнить, что следующая работа стартует в тот момент, когда закончится самая длительная из непосредственно предшествующих. На каждом шаге прямого анализа добавляется время выполнения расчетной операции. Так мы получаем значения раннего начала (ES) и раннего окончания работ (EF).

Но нужно быть внимательным: раннее окончание предшествующей операции становится ранним началом последующей только в том случае, если она не является слиянием. В этом случае стартом станет раннее окончание самой затяжной из предыдущих работ.

Минимизация числа исполнителей проекта при сохранении времени его выполнения

линейная диаграммакарта проекта

• минимизировать количество одновременно занятых исполнителей;
• выровнять потребность в трудовых ресурсах на протяжении всего срока выполнения проекта.

• перемещение работ по оси времени возможно осуществлять только вправо (откладывая их начало);
• работы критического пути трогать нельзя, т. к. это приведет к увеличению срока выполнения всего проекта;
• работы, имеющие свободный резерв времени, можно спокойно перемещать на величину этого резерва;
• перемещение работ, имеющих только полный резерв времени, требует аналогичного сдвига последующих работ;
• передвигаемые работы на линейной диаграмме выделяют, отмечая заметным символом: звездочкой, штрихом, цветом и т.п.

калькулятора

Таблица 1

Работа (ij)	Длительность t(ij), дн.	Количество исполнителей
1,2	4	5
2,3	6	3
2,4	5	6
2,7	11	6
3,5	9	1
4,6	9	2
5,7	11	3
6,7	10	5
7,8	4	6

Рис. 1. Пример сетевого графика

Проведем более детальный анализ линейной диаграммы и карты проекта с целью оптимизации трудовых ресурсов: выравнивая потребность в них на протяжении всего проекта и минимизируя количество одновременно занятых исполнителей. График ежедневной потребности ресурса показывает, что минимальное число исполнителей не может быть меньше 6 человек, что определяется их потребностью для работ критического пути. А 15 исполнителей на участке 5-10 дни проекта является явно завышенным и подлежит коррекции в первую очередь.

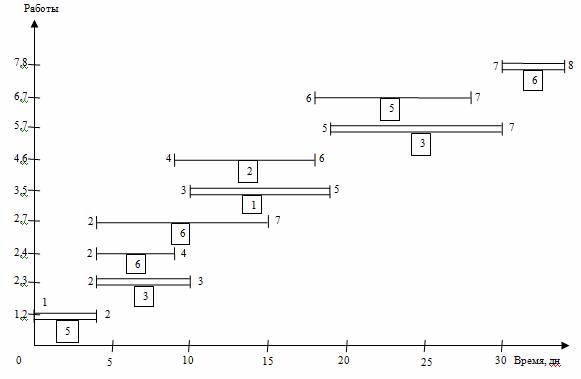
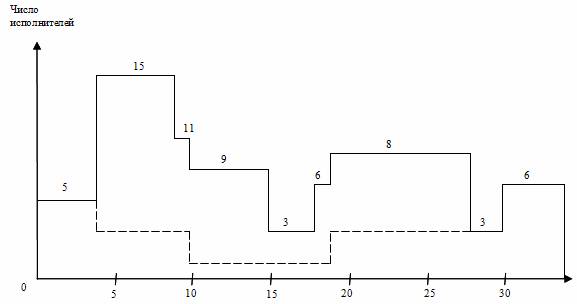Рис. 2. Линейная диаграмма и карта проекта до оптимизации

15 исполнителей заняты на работах 2,3; 2,4 и 2,7. Работу 2,3 трогать нельзя, т. к. это работа критического пути. Работа 2,4 имеет только полный резерв, но не имеет свободного резерва времени. Работа 2,7 имеет солидный свободный резерв времени и поэтому наиболее предпочтительна для оптимизации. Используем часть свободного резерва, переместив работу 2,7 (5-15 дни) на 5 дней (ее новый срок 10-20 дни). Тем самым максимально необходимое число исполнителей уменьшилось до 9 человек, т.е. задачу минимизации трудовых ресурсов проекта можно принять завершенной.

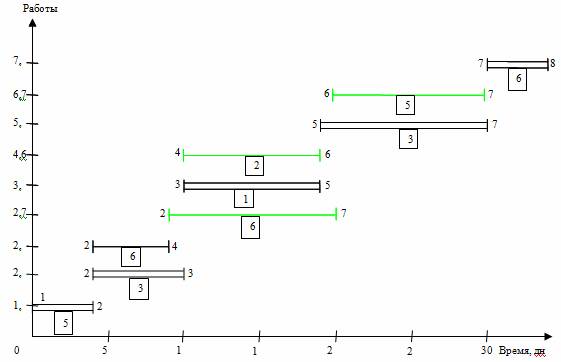
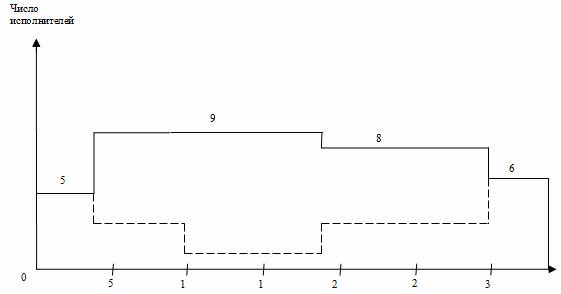
Рис. 3. Линейная диаграмма и карта проекта после оптимизации
Далее решим задачу выравнивания потребности в ресурсах, анализируя интервалы времени, связанные с «провалами» карты проекта. С учетом перемещения работы 2,7 падения спроса на исполнителей в середине проекта (16-18 дни) уже не будет, но он останется ближе к концу проекта (29-30 дни). Чтобы сгладить график загрузки, переместим работу 6,7 (19-28 дни), имеющую свободный резерв времени, на 2 дня (новый срок 21-30 дни). Также для целей выравнивания потребности в трудовых ресурсах переместим работу 4,6 (10-18 дни) на 1 день (11-19 дни).
В итоге оптимизации приходим к линейной диаграмме и карте проекта, представленными на рис. 3. Из графика видно улучшение равномерности загрузки исполнителей: новая ежедневная потребность ресурса составляет от 5 до 9 человек в зависимости от этапа выполнения проекта, резких колебаний занятости нет. Длительность выполнения всего проекта при этом осталась неизменной (34 дня), т. е. необходимое условие оптимизации соблюдено.

Видеоинструкция

Виды операций

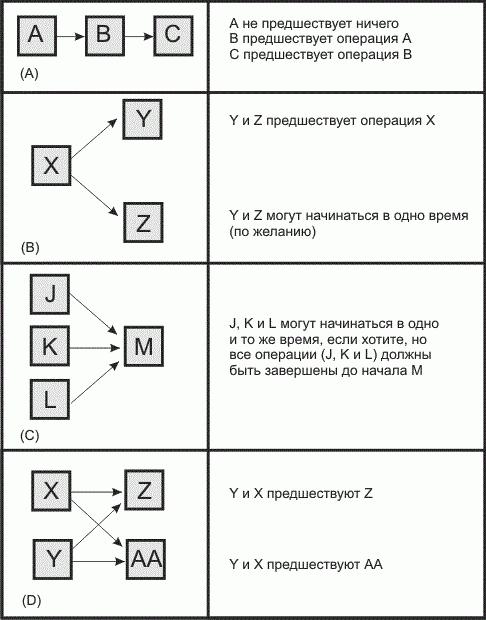
При составлении сетевого графика различают несколько видов работ:

• слияние – этой операции непосредственно предшествует больше, чем одна работа;
• параллельные операции выполняются независимо друг от друга и по желанию инженера-проектировщика могут выполняться одновременно;
• дробящаяся операция предполагает, что после ее выполнения можно выполнять сразу несколько не связанных между собой работ.

Кроме того, есть еще несколько необходимых для планирования понятий. Путь – это время на выполнение и последовательность взаимозависимых операций. А критическим путем называют самый длинный путь всей системы работ. В том случае, если какая-то операция на этом пути выполняется несвоевременно, срываются сроки реализации всего проекта.

И последнее: событие. Этим термином обычно обозначают начало или окончание какой-то операции. Событие не требует ресурсов.

Инструкция к сервису

Для добавления вершины на графическое полотно необходимо использовать соответствующую фигуре кнопку Добавить. Новый объект также можно вставить, предварительно выделив его левой кнопкой мыши, а затем щелкнуть мышкой на рабочем поле. Нумерация вершин может начинаться с 0, для этого нужно снять отметку с пункта Нумерация вершин с №1.

12341103015

Нумерация вершин с 0

01231103015

Чтобы соединить вершины, их необходимо предварительно выбрать (один клик мыши по объекту), а затем нажать на кнопку Соединить.Сетевая модель может быть представлена в табличной форме и в виде матрицы весов (матрицы расстояний). Чтобы использовать данные представления, выберите меню Операции.

Построенный граф можно сохранить в формате docx или png.Если в качестве формы вершин используется прямоугольник, то при построении секторальной диаграммы применяется методология Microsoft Visio с отображением параметров duration, ES, EF, LS, LF, and slack.

Основные определения

Ориентированный граф, в котором существует лишь одна вершина, не имеющая входящих дуг, и лишь одна вершина, не имеющая выходящих дуг, называется сетью. Сеть, моделирующая комплекс работ, называется его сетевой моделью или сетевым графиком. Дуги, соединяющие вершины графа, ориентированы в направлении достижения результата при осуществлении комплекса работ.Наиболее распространен способ представления моделируемого комплекса работ в понятиях работ и событий.Понятие «работа» имеет следующие значения:

• «действительная работа» – процесс, требующий затрат времени и ресурсов;
• «фиктивная работа» – логическая связь между двумя или несколькими работами, указывающая на то, что начало одной работы зависит от результатов другой. Фиктивная работа не требует затрат времени и ресурсов, продолжительность ее равна нулю.

Работа на графике изображается стрелкой, над которой указывается затрачиваемое на нее время. Длина стрелки и ее ориентация на графике не имеют значения. Желательно только выдерживать направление стрелок так, чтобы начальное событие для работы (обозначается i) располагалось слева в сетевом графике, а конечное (обозначается j) — справа. Для отображения фиктивных работ используют пунктирные стрелки, над которыми время не указывается или проставляется ноль.

На сетевой модели событиям соответствуют вершины графа.

Правила построения сетевой модели

Правило 1. Каждая операция в сети представляется одной и только одной дугой (стрелкой). Ни одна из операций не должна появляться в модели дважды. При этом следует различать случай, когда какая-либо операция разбивается на части; тогда каждая часть изображается отдельной дугой.

Правило 2. Ни одна пара операций не должна определяться одинаковыми начальным и конечным событиями. Возможность неоднозначного определения операций через события появляется в случае, когда две или большее число операций допустимо выполнять одновременно.

Правило 3. При включении каждой операции в сетевую модель для обеспечения правильного упорядочения необходимо дать ответы на следующие вопросы:а) Какие операции необходимо завершить непосредственно перед началом рассматриваемой операции?б) Какие операции должны непосредственно следовать после завершения данной операции?в) Какие операции могут выполняться одновременно с рассматриваемой?

При построении сетевого графика следует соблюдать следующие правила:

• в сети не должно быть «тупиков», т.е., событий, от которых не начинается ни одна работа, исключая завершающее событие графика;
• В сетевом графике не должно быть «хвостовых» событий, то есть событий, которым не предшествует хотя бы одна работа, за исключением исходного.
• в сети не должно быть замкнутых контуров (рис.1);
• Любые два события должны быть непосредственно связаны не более чем одной работой.
• В сети рекомендуется иметь одно исходное и одно завершающее событие.
• Сетевой график должен быть упорядочен. То есть события и работы должны располагаться так, чтобы для любой работы предшествующее ей событие было расположено левее и имело меньший номер по сравнению с завершающим эту работу событием.

Построение сетевого графика начинается с изображения начального события, которое обозначается цифрой 1 и обводится кружком. Из начального события выпускают стрелки, соответствующие работам, которым не предшествуют какие-либо другие работы. По определению, момент завершения работы является событием. Поэтому каждая стрелказавершается кружком – событием, в котором проставляется номер этого события. Нумерация событий произвольная. На следующем этапе построения изображаем работы, которым предшествуют уже нарисованные работы (то есть которые опираются на уже построенные работы) и т. д. На следующем этапе отражаем логические взаимосвязи между работами и определяем конечное событие сетевого графика, на которое не опираются никакие работы. Построение закончено, далее необходимо провести упорядочение сетевого графика.

Использование табличного метода

Общепризнанные ПП календарного планирования (MS Project, Primavera Suretrack, OpenPlan и т.п.) способны вычислять ключевые параметры сетевой модели проекта. Мы же в настоящем разделе табличным методом выполним настройку подобного расчета обычными средствами MS Excel. Для этого возьмем наш пример фрагмента проектных операций проекта в области СМР. Расположим основные параметры сетевого графика в столбах электронной таблицы.

Модель расчета параметров сетевого графика табличным способом

Преимуществом выполнения расчетов табличным способом является возможность простой автоматизации вычислений и избежание массы ошибок, связанных с человеческим фактором. Красным цветом будем выделять номера операций, располагающихся на критическом пути, а синим цветом отметим расчетные позиции частных резервов, превышающих нулевое значение. Разберем пошагово расчет параметров сетевого графика по основным позициям.

1. Ранние начала операций, следующих за текущей работой. Алгоритм расчета настраиваем на выбор максимального значения из раннего времени окончания нескольких альтернативных предыдущих действий. Взять, например, операцию под номером 13. Ей предшествуют работы 6, 7, 8. Из трех ранних окончаний (71, 76, 74 соответственно) нам нужно выбрать максимальное значение – 76 и проставить его в качестве раннего начала операции 13.
2. Критический путь. Выполняя процедуру расчета по пункту 1 алгоритма, мы доходим до конца фрагмента, найдя значение продолжительности критического пути, которая в нашем примере составила 120 дней. Значения наибольших ранних окончаний среди альтернативных действий обозначают операции, лежащие на критическом пути. Отмечаем эти операции красным цветом.
3. Поздние окончания операций, предшествующих текущей работе. Начиная с концевой работы начинаем движение в обратную сторону от действий с большими номерами к операциям с меньшими. При этом из нескольких альтернатив исходящих работ выбираем наименьшее знание позднего начала. Поздние начала вычисляем как разницу между выбранными значениями поздних окончаний и продолжительности операций.
4. Резервы операций. Вычисляем полные (общие) резервы как разницу между поздними началами и ранними началами либо между поздними окончаниями и ранними окончаниями. Значения частных (свободных) резервов получаем в результате вычитания из числа раннего начала следующей операции раннего окончания текущей.

Мы рассмотрели практические механизмы составления сетевого графика и расчета основных параметров временной продолжительности проекта. Таким образом, вплотную приблизились к исследованию возможностей анализа, проводимого с целью оптимизации сетевой модели и формирования непосредственно плана действий по улучшению ее качества. Настоящая тема занимает немного места в комплексе знаний проект-менеджера и не так уж и сложна для восприятия. Во всяком случае, каждый РМ обязан уметь воспроизводить визуализацию графика и выполнять сопутствующие расчеты на хорошем профессиональном уровне.

Временные параметры сетей. Резервы времени.

Основными
временными параметрами сетей являются
ранние и поздние сроки наступления
(совершения) событий. Зная их, можно
вычислить остальные параметры сети –
сроки начала и окончания работ и резервы
времени событий и работ.

Обозначим
–
продолжительность работы с начальным
событиемi

и конечным событием j
.

Ранний
срок


совершения событияj

определяется величиной наиболее
длительного отрезка пути от исходного
до рассматриваемого события, причем
,
агдеN
— номер
завершающего события. Правило вычисления:

где
максимум берется по всем событиям i
, непосредственно
предшествующим событию j

(соединены стрелками).

Поздний
срок


свершения
событияi
характеризует
самый поздний допустимый срок, к которому
должно совершится событие, не вызывая
при этом срыва срока совершения конечного
события. Правило вычисления:

где
минимум берется по всем событиям j
,
непосредственно следующим за событиемi
.

Поздние
сроки событий определяются «обратным
ходом», начиная с завершающего события,
с учетом соотношения
,
т. е. поздний и ранний сроки совершения
завершающего события равны между собой.

Резерв


событияi
показывает,
на какой предельно допустимый срок
может задержаться свершение событияi

без нарушения срока наступления
завершающего события:

.

События
лежащие на критическом пути (критические
события) резервов не имеют.

Существуют
различные методы расчета параметров
сети: табличный и графический.

Рассмотрим
графический метод.

При
расчетах сетевого графика каждый круг,
изображающий событие, делим диаметрами
на четыре сектора:

Пример 55. Рассмотрим
сеть проекта, представленную следующим
графиком.

На
графике события представлены кругами,
а работы стрелками. Робота может
обозначаться как буквой, надписанной
на графике рядом с соответствующей
работе стрелкой, либо через номера
событий из которых начинается и
заканчивается работа.

Найти
критический путь. Сколько времени
потребуется для завершения проекта?
Можно ли отложить выполнение роботы D

без отсрочки завершения проекта в целом?
Насколько недель можно отложить
выполнение работы C

без отсрочки завершения проекта в целом?

1
этап. При вычислении раннего срока
свершения события
перемещаемся
от исходного события 1 завершающему
событию 6.

.

В
событие 2 входит только одна работа:
.

Аналогично
.

В
событие 4 входят две работы →

Отсюда следует,
что критическое время выполнения проекта
= 22.

Внесем соответствующие
данные в сетевой график.

2
этап. При вычислении позднего
срока
t
п
(i
) свершения события
I

перемещаемся от завершающего события
6 к исходному событию 1 по сетевому
графику против направления стрелок.

.

Из
события 4 выходят две работы: (4, 5) и (4,
6). Поэтому определяем поздний срок
наступления события t
п
( 4)
по каждой
из этих работ:

Внесем полученные
данные в сетевой график.

3
этап. Вычисляем резерв

событияi
, то есть из
чисел, полученных на этапе 2, вычитаем
числа, полученные на этапе 1.

4
этап. У критических событий резерв
времени равен нулю, так как ранние и
поздние сроки их свершения совпадают.
Критические события 1, 2, 4, 5, 6 и определяют
критический путь 1-2-4-5-6, который по
определению должен быть самым
продолжительным по времени. На сетевом
графике мы его покажем двумя чертами.

Теперь можно
ответить на вопросы задачи.

Для
завершения проекта потребуется 22 недели.
Работа D

расположена на критическом пути. Поэтому
ее нельзя отложить без отсрочки завершения
проекта в целом. Работа C

не расположена на критическом пути, ее
можно задержать на
(недели).

Ход занятия:

Изучение нового материала.

Прежде чем непосредственно приступать к построению сетевого графика, составляют список всех работ, необходимых для выполнения заданного комплекса работ. Далее выясняют технологическую последовательность их выполнения; строят отдельные фрагменты сетевого графика; по возможности их упрощают. После этого из отдельных фрагментов строят общий сетевой график. В таких случаях принять говорить о «сшивании сетевого графика».

Познакомимся с основными правилами построения сетевых графиков:

1. Каждую стрелку в сетевом графике по возможности рисуют так, чтобы её конец находился правее начала, по возможности горизонтально.

2. Для удобства сетевой график строят без лишних пересечений стрелок. ( Вместе с тем при составлении чернового варианта не следует увлекаться внешним видом сети).

3. Следят за тем, чтобы во все вершины, кроме той, которая соответствует исходному событию, входила по меньшей мере одна стрелка, так как все события, кроме исходного, имеют предшествующую работу.

4. Следят за тем, чтобы из всех вершин сети, кроме той, которая соответствует завершающему событию, выходили стрелки, так как все события, кроме завершающего, имеют последующую работу.

5. Следят за тем, чтобы в сетевом графике не образовывалось циклов.

6. Если одно событие служит началом для двух или более работ, после завершения которых начинается выполнение следующей работы, то вводится штриховая стрелка (условная зависимость) и дополнительное событие со своим номером.

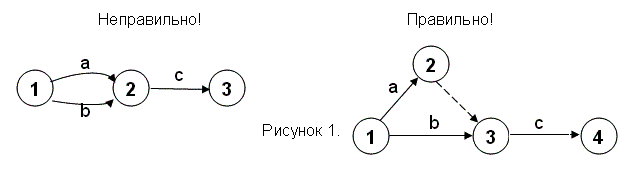
На рисунке 1 приведены неправильное и правильное изображения двух работ а и b, начинающихся после события 1; после завершения а и b начинается работа с.

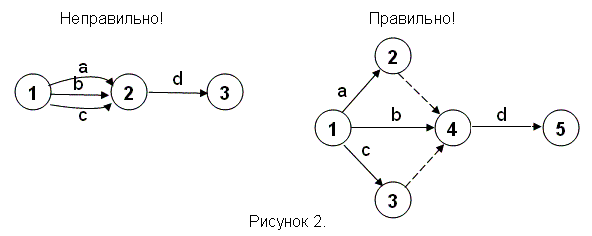
На рисунке 2 приведены неправильное и правильное изображения трёх работ а, b, с, начинающихся после события 1; после их завершения начинается работа d.

Правило 6 важно для расчётов сетевых графиков на компьютере, так как работы кодируются начальными и конечными событиями. При нарушении этого правила в памяти компьютера окажутся две или более одинаково закодированных работ

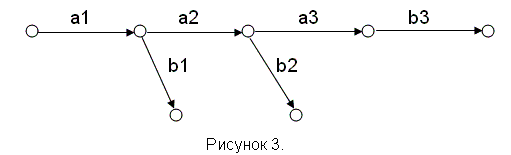
7. Если какие – то работы могут начаться до полного завершения предыдущей работы, то её следует разбить на части и считать каждую из них самостоятельной.

На рисунке 3 изображена часть сетевого графика. Здесь работа а разбита на 3 части а1, а2 и а3, причём после выполнения а1 начинается работа b1, после а2 – b2, после а3 – b3.

Такая ситуация может возникнуть, например, при проведении труб (водопроводных или газовых). Укладку труб можно производить по частям, не дожидаясь, когда будет готова траншея на всём участке.

8. На сетевом графике следует чётко отражать последовательность выполнения отдельных работ и их взаимосвязи. В помощь вводятся штриховые стрелки (условные зависимости) и дополнительные вершины (события).

Рассмотрим примеры построения отдельных фрагментов сетевых графиков.

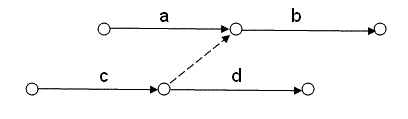
1) Четыре работы (а, b, с, d) связаны между собой следующей зависимостью:
b начинается после завершения работ а и с; d — после завершения работы с.

2) Пять работ (а, b, с, d, е) связаны между собой следующей зависимостью:
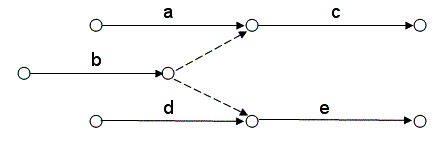
с начинается после завершения а и b; е – после окончания b и d.

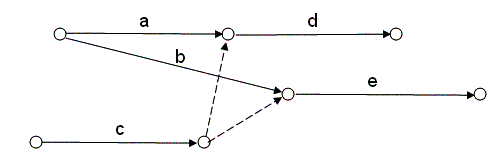
3) Пять работ (а, b, с, d, е) связаны между собой так: работы а и b начинаются после завершения каких – то одних и тех же работ; работу d можно начинать по окончании работ а и с; работу е – после завершения работ b и с.

Коллективное выполнение упражнений.

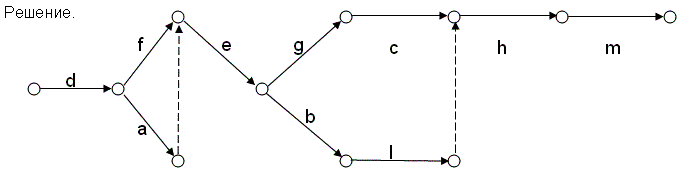
Упражнение 1. Ниже перечислены отдельные работы, которые выполняются при подготовке к туристическому походу.

а) Разработка маршрута похода.

b) Получение снаряжения.

с) Заготовка продуктов.

d) Формирование группы.

е) Утверждение руководителя группы и маршрута в совете по туризму.

f) Выбор руководителя группы и его помощников.

h) Получения разрешения на выход.

g) Сбор денег и получение дотации.

l) Проверка пригодности снаряжения и ремонт его.

m) Выход на маршрут.

Составьте сетевой график подготовки туристического похода. Используйте буквы, которыми обозначены отдельные работы в списке.

Упражнение 2. Ниже перечислены отдельные работы, которые выполняют при ремонте квартиры.

а) Шпаклёвка потолков и стен.

b) Побелка потолков.

c) Замена внешней электропроводки на внутреннюю.

d) Принятие решения о ремонте квартиры.

e) Договор с малярами.

f) Покупка материалов, необходимых для малярных работ.

h) Договор с электромонтёрами.

g) Оклеивание стен обоями.

l) краска дверей и оконных рам.

m) Покрытие полов лаком.

n) Уборка после завершения малярных работ.

o) Шпаклёвка дверей и оконных рам.

Составьте сетевой график ремонта квартиры. Используйте буквы, которыми обозначены отдельные работы в списке.

Решение: