Темп роста и темп прироста: определение и формулы расчета

Показатели динамики: темп роста и темп прироста

Темп роста (Тр) — это показатель интенсивности изменения уровня ряда, который выражается в процентах, а в долях выражается коэффициент роста (Кр).

Кр определяется как отношение последующего уровня к предыдущему или к показателю принятому за базу сравнения.

Он определяет, во сколько раз увеличился уровень по сравнению с базисным, а в случае уменьшения — какую часть базисного уровня составляет сравниваемый.

Рассчитываем коэффициент роста, умножаем на 100 и получаем темп роста

Коэффициент роста может быть рассчитан по формулам:

Также темп роста может определяться так:

Темп роста всегда положителен. Между цепным и базисным темпами роста существует определенная взаимосвязь: произведение цепных коэффициентов роста равно базисному коэффициенту роста за весь период, а частное от деления последующего базисного темпа роста на предыдущий равно цепному темпу роста.

Абсолютный прирост

Абсолютный прирост характеризует увеличение (уменьшение) уровня ряда за определенный промежуток времени. Он определяется по формуле:

1. Абсолютный прирост (цепной):

2. Абсолютный прирост (базисный):

где уi — уровень сравниваемого периода;

Уi-1 — Уровень предшествующего периода;

У0 — уровень базисного периода.

Цепные и базисные абсолютные приросты связаны между собой таким образом: сумма последовательных цепных абсолютных приростов равна базисному, т. е. общему приросту за весь промежуток времени:

Абсолютный прирост может быть положительным или отрицательным знак. Он показывает, на сколько уровень текущего периода выше (ниже) базисного, и таким образом измеряет абсолютную скорость роста или снижение уровня.

Темп прироста

Темп прироста (Тпр) показывает относительную величину прироста и показывает, на сколько процентов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения.

Он может быть как положительным, так и отрицательным или равным нулю, он выражается в процентах и долях (коэффициенты прироста); рассчитывается как отношение абсолютного прироста к абсолютному уровню, принятому за базу:

Темп прироста можно получить из темпа роста:

Коэффициент прироста может быть получен таким образом:

Абсолютное значение 1%-го прироста

Абсолютное значение 1% прироста (А%) — это отношение абсолютного прироста к темпу прироста, выраженный в процентах и показывает значимость каждого процента прироста за тот же период времени:

Абсолютное значение одного процента прироста равно сотой части предыдущего или базисного уровня. Оно показывает, какое абсолютное значение скрывается за относительным показателем — одним процентом прироста.

Примеры расчетов показателей динамики

Перед изучением теории по теме показатели динамики Вы можете посмотреть примеры задач по нахождению: темпа роста, темпа прироста, абсолютного прироста, средних величин динамики

Пример 1. Расчет среднемесячного темп роста объема продаж

Пример 2. Определение всех показателей динамики (подробный расчет)

Пример 3. Расчет цепных, базисных и средних показателей динамики

О показателях динамики

При исследовании динамики общественных явлений возникает трудность описания интенсивности изменения и расчета средних показателей динамики в контрольных по статистике, которые задают студентам.

Анализ интенсивности изменения во времени происходит с помощью показателей, которые получаются вследствие сравнения уровней. К этим показателям относят: темп роста, абсолютный прирост, абсолютное значение одного процента прироста.

Для обобщающей характеристики динамики исследуемых явлений определяется средний показатели: средние уровни ряда и средние показатели изменения уровней ряда. Показатели анализа динамики могут определяться по постоянной и переменным базам сравнения.

Здесь принято называть сравнимый уровень отчетным, а уровень, с которого производится сравнение, — базисным.

Для расчета показателей динамики на постоянной базе, нужно каждый уровень ряда сравнить с одним и тем же базисным уровнем.

В качестве базисного используют только начальный уровень в ряду динамики или уровень, с которого начинается новый этап развития явления. Показатели, которые при этом рассчитываются, называются базисными.

Для расчета показателей анализа динамики на переменной базе нужно каждый последующий уровень ряда сравнить с предыдущим. Вычисленные показатели анализа динамики будут называться цепными.

Как рассчитать динамику показателей | Сделай все сам

Обзор динамики показателей начинается с того, как именно они изменяются (возрастают, уменьшаются либо остаются постоянными) в безусловном и относительном выражении. Дабы проследить за изменением рядов динамики во времени, рассчитываются показатели: безусловное метаморфоза, относительное метаморфоза, темп метаморфозы.

Инструкция

1. Учтите, что все данные показатели могут быть базисными, когда ярус одного периода сравнивается с ярусом исходного периода, и цепными, когда сравнивается ярус 2-х соседних периодов.

2. Базисное безусловное метаморфоза (безусловный приход) вы можете рассчитать как разность определенного и первого ярусов ряда: У(б) = У(i ) – У(1). Оно показывает, насколько ярус определенного периода огромнее либо поменьше базисного яруса.

Цепное безусловное метаморфоза – это разность между определенным и предыдущим ярусом ряда: У (ц) = У(i) – У(i-1). Оно показывает, на сколько единиц ярус определенного периода огромнее либо поменьше предыдущего.

Помните, что между базисным и цепным безусловным изменением существует связь: сумма цепных безусловных изменений равна последнему базисному изменению.

3.

При обзоре динамики показателей вы можете рассчитать базисное относительное метаморфоза (базисный темп роста). Он представляет собой отношение определенного показателя к первому из ряда динамики: I(б) = У(i)/Y(1). Цепное относительное метаморфоза – это соотношение определенного и предыдущего яруса ряда: I(ц) = У(i)/Y(i-1).

Относительное метаморфоза показывает, во сколько раз ярус данного ряда огромнее яруса предыдущего ряда либо какую часть его часть составляет. Относительное метаморфоза может выражаться в процентах, путем умножения соотношения на 100 %.

4. Помимо того, при обзоре динамики показателей вы можете рассчитать темп метаморфозы (темп прихода) ярусов.

Это относительный показатель, тот, что показывает, на сколько процентов данный показатель огромнее либо поменьше иного, принимаемого за базу сопоставления.

Он определяется путем вычитания из относительного базисного либо цепного метаморфозы 100%: Т(i) = I(i) – 100%.

Совет 2: Как рассчитать относительные показатели

Относительные показатели предуготовлены для того, дабы характеризовать интенсивность протекающих изменений измеряемой величины.

Для их нахождения нужно знать безусловные значения как минимум в 2-х точках измерений – скажем, на 2-х отметках временной шкалы.

Следственно относительные показатели считаются вторичными по отношению к безусловным, но тем не менее, без них сложно оценить всеобщую картину изменений, протекающих с измеряемым параметром.

Совет 3: Как рассчитать динамику

Динамика по своей сути – это показатель движения процесса в правильную либо негативную сторону. Она фиксирует становление события, процесса, явления и т.п. Следственно для расчета динамики какого-нибудь процесса необходимо вооружиться основными его показателями.

Скажем, для того, дабы произвести количественную оценку динамики общественно-экономических явлений возьмите следующие статистические показатели: приход, темп роста, темп наращивания и др. Как вы могли подметить, все эти показатели отражают в себе движение.

Оно заложено в определении динамики.

Совет 4: Как рассчитать безусловный прирост

Для определения интенсивности изменений каких-нибудь показателей за определенный период времени применяется комплект колляций, которые получаются способом сопоставления нескольких ярусов показателей, измеренных на различных отметках временной шкалы. В зависимости от того, каким образом сравниваются измеренные показатели между собой, полученные колляции именуются показателем роста, темпом роста, темпом прихода, безусловным приходом либо безусловным значением 1% прихода.

Преимущества и недостатки

Основными преимуществами показателя совокупного среднегодового темпа роста являются простота его применения и универсальность подхода. Он позволяет провести сравнение любых объектов инвестирования вне зависимости от их природы, формы деятельности и технологии достижения финансовых результатов.

Действительно, даже такие варианты, как фьючерсы на различные товары и фондовые индексы могут анализироваться в однородных условиях с применением CAGR. Кроме того, его способности к фильтрации результатов позволяют избавиться от малозначимой информации (например, рыночного шума) при работе с долгосрочными проектами.

Однако, присущи ему, как и всем проводящим усреднение инструментам, определенные недостатки:

Анализ с применением CAGR предполагает наличие устойчивой тенденции изменения исследуемого параметра (например, роста цены акций или доходности инвестиций)
При рассмотрении игнорируется такое важное свойство, как волатильность, которая может приводить к значительному изменению внутри отчетного периода, и, соответственно влиять на инвестиционные риски.
CAGR хорошо работает на исторических данных

Однако, распространять полученные с его использование оценки на будущие периоды следует с осторожностью – гарантии, что тенденция сохраниться нет, да и количественные результаты обладают невысокой надежностью.
Расчетные соотношения делают показатель весьма чувствительным к выбору отчетного периода
Специалист может представить выборку для анализа таким образом, что инвестор получит информацию о превосходных результатах компании, в то время как более тщательный анализ сообщит о кризисных явлениях.. Словом, простой и удобный инструмент стоит того, чтобы применять его широко

Однако, не стоит забывать, что показатель этот искусственно создан, и принимать решения только на его базе недопустимо

Словом, простой и удобный инструмент стоит того, чтобы применять его широко. Однако, не стоит забывать, что показатель этот искусственно создан, и принимать решения только на его базе недопустимо.

Показатели изменения уровней ряда динамики

Анализ рядов динамики начинается с определения того, как именно изменяются уровни ряда (увеличиваются, уменьшаются или остаются неизменными) в абсолютном и относительном выражении. Чтобы проследить за направлением и размером изменений уровней во времени, для рядов динамики рассчитывают показатели изменения уровней ряда динамики:

• абсолютное изменение (абсолютный прирост);
• относительное изменение (темп роста или индекс динамики);
• темп изменения (темп прироста).

Все эти показатели могут определяться базисным способом, когда уровень данного периода сравнивается с первым (базисным) периодом, либо цепным способом – когда сравниваются два уровня соседних периодов.

Базисное абсолютное изменение представляет собой разность конкретного и первого уровней ряда, определяется по формуле

Оно показывает, на сколько (в единицах показателей ряда) уровень одного (i-того) периода больше или меньше первого (базисного) уровня, и, следовательно, может иметь знак «+» (при увеличении уровней) или «–» (при уменьшении уровней).

Цепное абсолютное изменение представляет собой разность конкретного и предыдущего уровней ряда, определяется по формуле

Оно показывает, на сколько (в единицах показателей ряда) уровень одного (i-того) периода больше или меньше предыдущего уровня, и может иметь знак «+» или «–».

В в столбце 3 рассчитаны базисные абсолютные изменения, а в столбце 4 – цепные абсолютные изменения.

Год	y					, %	,%
2004	144,2
2005	143,5	-0,7	-0,7	0,995	0,995	-0,49	-0,49
2006	142,8	-1,4	-0,7	0,990	0,995	-0,97	-0,49
2007	142,2	-2,0	-0,6	0,986	0,996	-1,39	-0,42
2008	142,0	-2,2	-0,2	0,985	0,999	-1,53	-0,14
2009	141,9	-2,3	-0,1	0,984	0,999	-1,60	-0,07
Итого			-2,3		0,984		-1,60

Между базисными и цепными абсолютными изменениями существует взаимосвязь: сумма цепных абсолютных изменений равна последнему базисному изменению, то есть

.

Базисное относительное изменение (базисный темп роста или базисный индекс динамики) представляет собой соотношение конкретного и первого уровней ряда, определяясь по формуле

Цепное относительное изменение (цепной темп роста или цепной индекс динамики) представляет собой соотношение конкретного и предыдущего уровней ряда, определяясь по формуле

.

Относительное изменение показывает во сколько раз уровень данного периода больше уровня какого-либо предшествующего периода (при i>1) или какую его часть составляет (при i<1). Относительное изменение может выражаться в виде коэффициентов, то есть простого кратного отношения  (если база сравнения принимается за единицу), и в процентах (если база сравнения принимается за 100 единиц) путем домножения относительного изменения на 100%.

Между базисными и цепными относительными изменениями существует взаимосвязь: произведение цепных относительных изменений равно последнему базисному изменению, то есть

.

Темп изменения (темп прироста) уровней – относительный показатель, показывающий, на сколько процентов данный уровень больше (или меньше) другого, принимаемого за базу сравнения. Он рассчитывается путем вычитания из относительного изменения 100%, то есть по формуле:

,

.

Виды рядов динамики

В зависимости от характеризующего критерия, существует несколько разновидностей динамических рядов.

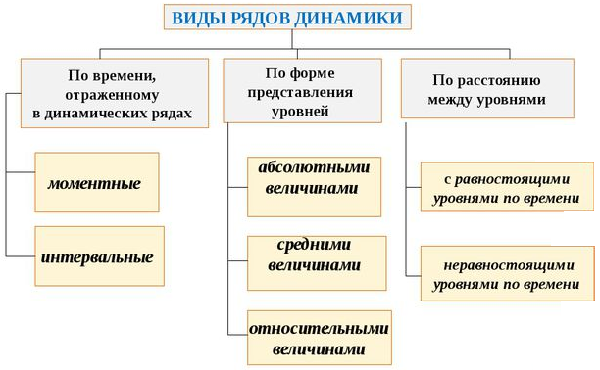
По временной характеристике различают моментальные и интервальные:

1. Для интервальных рядов характерна результативность. Иными словами такой ряд может состоять из суммарной характеристики, которая произошла на данный момент времени t (например, сколько продукции произведено на момент времени, сколько человеко-дней зарегистрировано за определенный период).
2. Для моментальных рядов характерно мгновенное значение изучаемой характеристики. К таковым относится, например, объем запаса на требуемое время, затраты времени на временной интервал и др.

При характеристике по показателю t выделяют неполные и полные ряды. Неполными считаются такие, в которых не соблюдается одинаковый промежуток между соседними значениями времени. Для полных, такой интервал соблюден.

Кроме этого, существует классификация по количеству показателей. Существуют изолированные – во времени анализируется всего один показатель и многомерные, когда во времени анализ ведется для целого ряда параметров, которые связаны между собой одним процессом.

Как рассчитать темп роста и прироста?

Темп роста – это прирост какой-либо изучаемой величины за один временной период (обычно применяется к году).

Темп прироста – это прирост какой либо изучаемой величины за один временной период за вычетом 100%.

Темп роста и темп прироста измеряются в процентах и являются относительными величинами. Темп роста – всегда величина положительная, темп прироста может быть отрицательным. Темп прироста равен темп роста минус 100%.

Теперь рассмотрим расчет темпа роста и темпа прироста более подробно.

Помогу разобраться с расчетами темпа роста и прироста ОНЛАЙН ЗДЕСЬ

Расчет темпа роста и прироста

Для наглядности СКАЧАЙТЕ ФАЙЛ РАСЧЕТА, в котором отражен расчет: темп роста и темп прироста

Обратите внимание: на первом листе книги файла расчетов представлен расчет, а на втором листе книги файла расчетов – формулы расчета темпа роста и прироста

На рисунке представлен пример расчета темпа роста и прироста:

Для наглядности на рисунке ниже приведен этот же пример, только с открытыми формулами:

На рисунке видно, что определение темпа роста осуществляется путем деления Показателя 2 на Показатель 1 и умножения на 100%. При этом темп прироста равен: деление показателя 2 на показатель 1 умножение на 100% и минус 100%, то есть темп прироста равен темп роста минус 100%.

Расчет средних темпов роста и прироста

Так же на рисунках указано как рассчитывается средний темп роста и средний темп прироста. Для определения среднего темпа роста необходимо сложить показатели за все четыре периоды и разделить полученную сумму на количество периодов, то есть на 4. Аналогично рассчитывается средний темп прироста – сумма темпов прироста за все периоды делится на количество периодов.

Помогу разобраться с расчетами темпа роста и прироста ОНЛАЙН ЗДЕСЬ

Расчет базисного темпа роста и базисного темпа прироста

Для наглядности СКАЧАЙТЕ ФАЙЛ РАСЧЕТА, в котором отражен расчет: базисный темп роста, базисный темп прироста, цепной темп роста, цепной темп прироста

Обратите внимание: на первом листе книги файла расчетов представлен расчет, а на втором листе книги файла расчетов – формулы расчета темпа роста и прироста

На рисунке ниже представлен расчет базисного темпа роста и прироста (таблицы 2 и 3):

Расчет базисного темпа роста заключается в том, что необходимо произвести расчет темпов роста всех показателей

Обратите внимание, что тем роста (прироста) первого показателя рассчитать нельзя

Помогу разобраться с расчетами темпа роста и прироста ОНЛАЙН ЗДЕСЬ

В примере за базисный показатель принят Показатель 1, поэтому базисный темп роста или базисный темп прироста рассчитывается исходя из этого положения, то есть при расчете базисного темпа роста Показатель 2 делим на Показатель 1 и умножаем на 100, далее Показатель 3 делим на Показатель 1 и умножаем на 100, далее Показатель 3 делим на Показатель 1 и умножаем на 100, при расчете базисного темпа прироста из каждого показателя базисного темпа роста вычитаем 100.

Расчет цепного темпа роста и цепного темпа прироста

На рисунке выше представлен расчет базисного темпа роста и прироста (таблицы 4 и 5).

Расчет цепного темпа роста заключается в том, что необходимо произвести расчет темпов роста всех показателей

Обратите внимание, что тем роста (прироста) первого показателя рассчитать нельзя. В отличие от базисного темпа роста или прироста, цепной темп роста или прироста рассчитывается из текущего и предыдущего показателя

То есть цепной темп роста или цепной темп прироста рассчитывается следующим образом: Показатель 2 делим на Показатель 1 и умножаем на 100, далее Показатель 3 делим на Показатель 2 и умножаем на 100, далее Показатель 4 делим на Показатель 3 и умножаем на 100, при расчете цепного темпа прироста из каждого показателя цепного темпа роста вычитаем 100.

Для того, чтобы закрепить полученную информацию, обратите внимание на рисунок ниже, в котором отражены формулы расчета: базисный темп роста, базисный темп прироста, цепной темп роста, цепной темп прироста:

Помогу разобраться с расчетами темпа роста и прироста ОНЛАЙН ЗДЕСЬ

3.1. Понятие выборки (применительно к исследованию в психологии)

3.2. Не любите проводить социологическое исследование? Вы просто не умеете его готовить!

3.3. Корреляционный анализ по методу Спирмена (ранги Спирмена)

3.4. Дискуссия: Объект и Предмет исследования или наоборот?

3.5. Решение задач по праву. Как решить задачу по Юриспруденции?

3.6. Как рассчитать темп роста и прироста?

3.7. Как выбрать тему дипломной работы?

3.8. Методы исследования в дипломе, пример

Расчет темпа прироста в табличном редакторе

Цепной темп роста обозначает отношение процента к предыдущему показателю. Формула цепного темпа роста выглядит следующим образом:

7

Базисный темп роста обозначает отношение процента к базисному показателю. Формула базисного темпа роста выглядит следующим образом:

8

Предыдущий показатель – это показатель в прошедшем квартале, месяце и так далее. Базисный показатель – это начальный показатель. Цепной тем прироста – это вычисляемая разница между 2 показателями (настоящий и прошлый). Формула цепного темпа прироста выглядит следующим образом:

9

Базисный темп прироста – это вычисляемая разница между 2 показателями (настоящий и базисный). Формула базисного темпа прироста выглядит следующим образом:

10

Рассмотрим все детально на конкретном примере. Подробная инструкция выглядит так:

1. К примеру, у нас есть такая табличка, отражающая доход по кварталам. Задача: вычислить темпы прироста и роста.

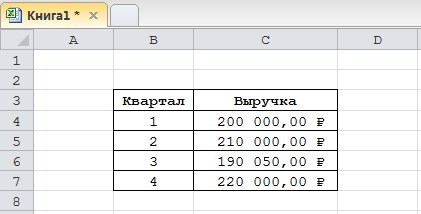11

1. Первоначально реализуем добавление четырех колонок, в которых будут содержаться вышеприведенные формулы.

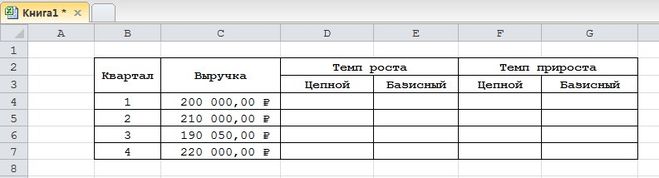12

1. Мы уже выяснили, что такие значения высчитываются в процентах. Нам необходимо задать для таких ячеек процентный формат. Жмем на необходимый диапазон правой клавишей мышки. В возникшем маленьком специальном контекстном меню необходимо выбрать кнопку, имеющую наименование «Формат ячеек». Здесь необходимо щелкнуть левой клавишей мышки на элемент «Формат», а затем при помощи кнопки «ОК», сохранить внесенные изменения.
2. Вводим такую формулу для подсчета цепного темпа роста и копируем в нижние ячейки.

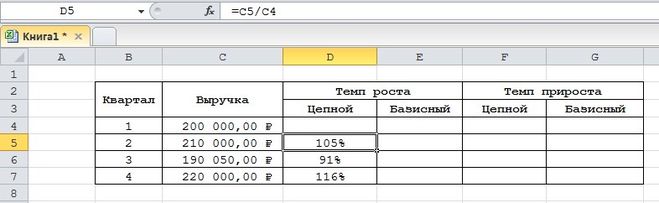13

1. Вводим такую формулу для базисного цепного темпа роста и копируем в нижние ячейки.

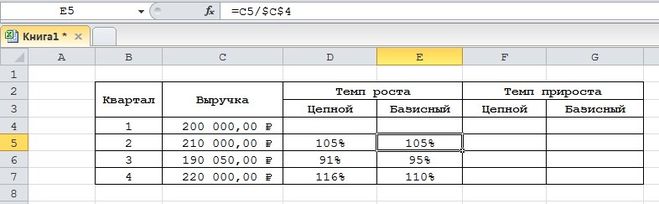14

1. Вводим такую формулу для подсчета цепного темпа прироста и копируем в нижние ячейки.

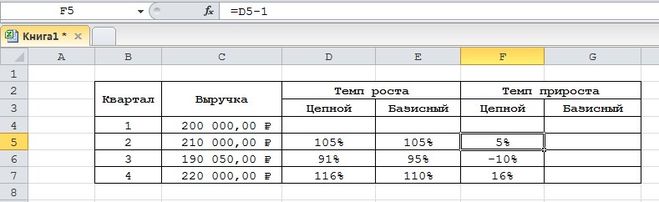15

1. Вводим такую формулу для базисного цепного темпа прироста и копируем в нижние ячейки.

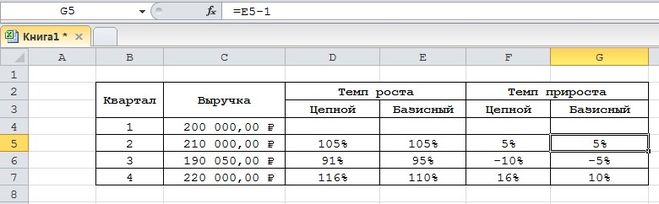16

1. Готово! Мы реализовали подсчет всех необходимых показателей. Вывод по нашему конкретному примеру: в 3 квартале плохая динамика, так как темп роста составляет сто процентов, а прирост положительный.

Виды рядов динамики

Ряды динамики классифицируются по следующим основным признакам:

1. По времени — ряды моментные и интервальные (периодные), которые показывают уровень явления на конкретный момент времени или на определенный его период. Сумма уровней интервального ряда дает вполне реальную статистическую величину за несколько периодов времени, например, общий выпуск продукции, общее количество проданных акций и т.п. Уровни моментного ряда, хотя и можно суммировать, но эта сумма реального содержания, как правило, не имеет. Так, если сложить величины запасов на начало каждого месяца квартала, то полученная сумма не означает квартальную величину запасов.
2. По форме представления — ряды абсолютных, относительных и средних величин.
3. По интервалам времени — ряды равномерные и неравномерные (полные и неполные), первые из которых имеют равные интервалы, а у вторых равенство интервалов не соблюдается.
4. По числу смысловых статистических величин — ряды изолированные и комплексные (одномерные и многомерные). Первые представляют собой ряд динамики одной статистической величины (например, индекс инфляции), а вторые — нескольких (например, потребление основных продуктов питания).

Понятие рядов динамики (временных рядов)

Одной из важнейших задач статистики является изучение изменений анализируемых показателей во времени, то есть их динамика. Эта задача решается при помощи анализа рядов динамики (временных рядов).

Ряд динамики (или временной ряд) – это числовые значения определенного статистического показателя в последовательные моменты или периоды времени (т.е. расположенные в хронологическом порядке).

Числовые значения того или иного статистического показателя, составляющего ряд динамики, называют уровнями ряда и обычно обозначают буквой y. Первый член ряда y₁ называют начальным или базисным уровнем, а последний y_n – конечным. Моменты или периоды времени, к которым относятся уровни, обозначают через t.

Ряды динамики, как правило, представляют в виде или , причем по оси абсцисс строится шкала времени t, а по оси ординат – шкала уровней ряда y.

Пример ряда динамики

Таблица. Число жителей России в 2004-2009 гг. в млн.чел, на 1 января

Год	2004	2005	2006	2007	2008	2009
Число жителей	144,2	143,5	142,8	142,2	142,0	141,9

График ряда динамики числа жителей России в 2004-2009 гг. в млн.чел, на 1 января

Данные и наглядно иллюстрируют ежегодное снижение числа жителей России в 2004-2009 годах.

Вычисление изменения в процентах при помощи формулы прироста

При помощи табличного редактора можно реализовать процедуру сравнения 2 долей. Для осуществления этого действия отлично подходит формула прироста. Если пользователю необходимо произвести сравнение числовых значений А и В, то формула будет иметь вид: =(В-А)/А=разница. Разберемся во всем более детально. Подробная инструкция выглядит так:

1. В столбике А располагаются наименования товаров. В столбике В располагается его стоимость за август. В столбике С располагается его стоимость за сентябрь.
2. Все необходимые вычисления будем производить в столбике D.
3. Выбираем ячейку D2 при помощи левой клавиши мышки и вводим туда такую формулу: =(С2/В2)/В2.

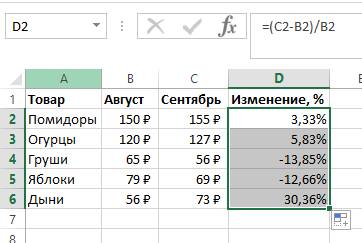4

1. Наводим указатель в нижний правый уголок ячейки. Он принял форму небольшого плюсика темного цвета. При помощи зажатой левой клавиши мышки производим растягивание этой формулы на всю колонку.
2. Если же необходимые значения находятся в одной колонке для определенной продукции за большой временной промежуток, то формула немножко изменится. К примеру, в колонке В располагается информация за все месяцы продаж. В колонке С необходимо вычислить изменения. Формула примет такой вид: =(В3-В2)/В2.

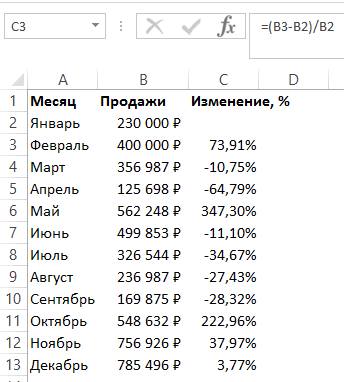5

1. Если числовые значения необходимо сравнить с определенными данными, то ссылку на элемент следует сделать абсолютной. К примеру, необходимо произвести сравнение всех месяцев продаж с январем, тогда формула примет такой вид: =(В3-В2)/$В$2. С помощью абсолютной ссылки при перемещении формулы в другие ячейки, координаты зафиксируются.

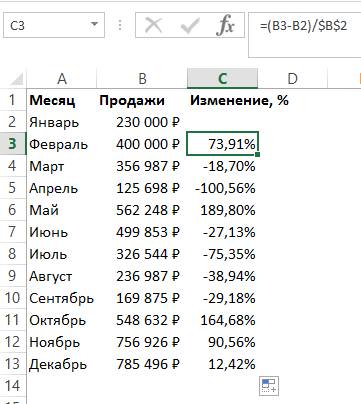6

1. Плюсовые показатели указывают на прирост, а минусовые – на уменьшение.

Анализ сезонных колебаний

Если взять для анализа временной ряд, в котором собраны объемы продаж противовирусных препаратов за 5 лет, то будет очевидно, что ежегодно происходят колебания (снижение или увеличение) продаж, которые повторяются. Такие колебания будут именоваться сезонными.

Чтобы устранить нежелательное влияние таких колебаний, проводится аналитическое изучение, выполняющееся либо с помощью гармонического исследования, либо с учетом индекса сезонности.

Индекс сезонности это фактическая характеристика того, в какое количество раз анализируемый уровень увеличен или уменьшен относительно срединного:

Тут Yt – это уровень, предполагаемый к анализу, а Ȳ это средний уровень всего ряда.

Более сложный анализ предполагает выделение гармонических колебаний. Для этого производится выравнивание по ряду Фурье (так называемые «гармоники»), и высчитывают, какие гармоники наиболее сопоставимы с анализируемым рядом. Общий вид ряда Фурье для двух гармоник выражается формулой:

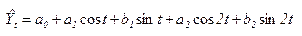
Индекс сезонности

Для того чтобы не вычислять относительную разницу в процентах между каждым месяцем во временном ряду, можно вычислить один параметр – индекс сезонности.

Индекс сезонности рассчитывается на основании следующих показателей:

• среднего по анализируемому показателю в указанный временной промежуток за три и более года (yi),
• среднего значения анализируемого показателя внутри одного временного периода (года) – y.

По результатам сопоставления получается значение, которое так или иначе соотносится с уровнем в 100%. Если присутствует значимое отклонение в меньшую сторону, то это является свидетельством присутствия сезонного колебания.

Приведение рядов динамики к одинаковому основанию

Во время работы с несколькими явлениями, описывающими один процесс, может вызывать интерес сопоставление рядов динамики. С целью корректного сопоставления потребуется приведение к одному основанию. Сопутствующей операцией является вычисление коэффициента опережения или отставания.

К каждому ряду находится базисный уровень и вычисляются темпы роста и прироста рядов. Для каждого ряда должен быть выбран аналогичный временной интервал.

Сравнение проводится на основании отношения базисного темпа роста (опционально – прироста) в аналогичном временной интервале. Выражения для расчета достаточно просты:

Показатели анализа рядов динамики

Всего имеются 5 характеристик, предназначающихся для выполнения анализа:

абсолютный прирост – это параметр, получающийся при нахождении разности определенного уровня и базисного (или тем, который следует до него). Возможен ответ со знаком «-». Выражения для расчета выглядят так:

коэффициент роста – значение, которое характеризует, в какое количество раз увеличился (или снизился) конкретно взятый для анализа уровень по сравнению с базисным или любым другим (например, идущим перед выбранным). Формула сводится к делению значения анализируемого уровня на значение базисного (отношение уровней):

• темп роста – характеризует процентное соотношение анализируемого показателя в сопоставлении с базисным. Вычисления выполняются перемножением значения коэффициента роста на сто процентов,
• темп прироста – процентный порог возрастания или снижения значения уровня в сопоставлении с базисным. При обсчете необходимо из 100 вычесть показатель темпа роста,
• абсолютное значение 1% прироста будет получено при делении абсолютного прироста на темп прироста. Эти характеристики не относятся к обязательным элементам.

Практические навыки

ТР. показывает, сколько процентов составляет одно число от другого. С помощью ТП можно вычислить, на сколько процентов возросло или сократилось число относительно другого.

Использование формул

ТР не бывает отрицательным, а ТП может. ТП определяется на базе ТР, обратный порядок недопустим. Чтобы высчитать величину, применяется ПП, поскольку он наглядно отражает динамику изменений.

Можно на примере посчитать темп роста в процентах. Работник завода получал заработную плату каждый месяц в зависимости от выработки. В январе сотрудник получил 40000 рублей, в феврале 45000 р. ТР составляет по формуле: 45000/40000*100 = 112,5. Таким образом, в феврале доход относительно предыдущего месяца может исчисляться как 112%.

Формулы широко применяются в повседневной жизни населения. В интернете имеется онлайн-калькулятор, позволяющий получить реальный результат или проверить собственные решения. Их использование позволяет опустить ошибки расчетов.

Разные методы расчета

Наглядное использование формул на примере позволит проанализировать предназначение ТР и ТП. В таблице представлен внутренний валовой продукт России с 2010—2017 годы. Необходимо найти ТР (в процентах) базисным и цепным методами.

Таблица данных о ВВП в национальной валюте за 2011−2018 гг.

Период	ВВП России ТР	(%)
в млрд р.	Цепной метод	Базисный метод
2011	48 000	–	–
2012	57 698	120,2	120,2
2013	66 817	115,8	139,2
2014	71 117	106,4	148,2
2015	78 945	111,0	164,5
2016	80 826	102,4	168,4
2017	83 871	103,8	174,7
2018	88 177	105,1	183,7

Формула цепного метода: ТР= Yi / Yi -1*100.

Для 2011 величины не будет. Начиная с 2012 года: 57698/48000*100 = 120,2%. Для 2013 года: 66817/57698*100 = 115,8%. Таким способом высчитываются суммы для каждого периода.

Базисный метод: ТР = Yi/Ybasic*100. Это отношение к основному, первому коэффициенту. Например, для 2012 года суммы высчитываются 57698/48000*100 = 120,2%, для 2013 года: 66817/48000*100 = 115,8%. Таким принципом вычисляются все оставшиеся периоды.

Таким же способом рассчитывается процентное соотношение данных актива баланса, отчета о прибылях и убытках. Показатели, отражающие величину чистой прибыли за 2 года, позволят выявить прирост или снижение показателей.

Данные	2017	2018	ТР %
Выручка от реализации	1500000	1600000	106,7
Финансовые доходы	400000	350000	87,5

За 2018 год ТР составит 106,7% выручки, а доходы от вложений возросли на 87,5%.

ТР необходим, чтобы узнать, сколько процентов составляет одно значение от другого. Последним выступает предыдущее число. Темп прироста позволяет выяснить, насколько изменился заданный параметр.

На основе одного из коэффициентов нельзя составить верную оценку определяемому явлению (по международному, отечественному рынку, предприятию, показателю работоспособности фирмы). Необходимы комплексные меры изучения и расчетов показателей в динамике. Для анализа финансовой деятельности можно брать разную информацию из форм отчетности.

Что подразумевают, когда говорят «темп прироста»?

Когда говорят о показателе темпа прироста, подразумевают, на какую величину процентов был увеличен или уменьшен показатель по сравнению с базисным или предыдущим периодом. Так, если начальное значение было 100 единиц продукции, а сейчас изготавливается 110, то темп прироста составляет 10%. Но может быть и такое, что в результате будет получено отрицательное значение. В таком случае можно говорить о темпе уменьшения анализируемого показателя, а не о приросте. Так, если начальное значение было в виде 100 единиц продукции, а при подсчете только 90, то уровень снижения составляет 10%.

Но какое уравнение нужно, чтобы рассчитать темп прироста? Формула выглядит так: абсолютный прирост делится на уровень предшествующего периода и умножается на сто процентов. Есть отдельные нюансы подсчета, которые разнятся в зависимости от объекта подсчета. Есть подсчет для собственного капитала, среднегодовой. Как узнать их темп прироста? Формула и особенности будут далее.

Ограничения на среднегодовой темп роста (AAGR) в финансовом анализе

Рассмотрим портфель, который вырастет на 25% в первый год и на 12% в следующий год. Среднегодовой темп роста (AAGR) будет рассчитан как 18,5%. Колебания доходности портфеля между началом первого года и концом года не учитывают расчет среднегодовых темпов роста.

Это может привести к определенным ошибкам в оценке. Поскольку AAGR представляет собой среднее значение годовой доходности, этот показатель не дает оценки общего риска, связанного с инвестициями, на основании нестабильности их цены. В принципе, AAGR можно оценить для любых инвестиций; однако он не будет указывать на потенциальный риск инвестиций.

Кроме того, AAGR не учитывает эффекты начисления процентов, поскольку это линейный показатель. Анализ может показать, что инвестиции росли в среднем на n процентов в год, при этом не учитывались колебания, которые могли произойти в течение временного ряда.

AAGR, идеально подходящий для отображения тенденций, также может вводить в заблуждение инвесторов, поскольку не отражает адекватно меняющиеся финансовые тенденции. Также можно переоценить рост инвестиций.

Дополнительные ресурсы:

Finansistem является официальным поставщиком глобальной программы сертификации специалистов по финансовому моделированию и оценке (FMVA) , призванной помочь каждому стать финансовым аналитиком мирового уровня. Чтобы продолжать учиться и продвигаться по карьерной лестнице, вам будут полезны следующие дополнительные ресурсы CFI:

• Управление активами
• Повышение цен
• Норма прибыли
• Инвестиционный портфель